题目内容

8．已知（tanα-3）（sinα+cosα+3）=0，求值：
（1）$\frac{4sinα+2cosα}{5cosα+3sinα}$
（2）$2+\frac{2}{3}{sin^2}α+\frac{1}{4}{cos^2}α$．

分析 （1）先求得tanα的值，再利用同角三角函数的基本关系，求得要求式子的值．
（2）利用同角三角函数的基本关系，求得要求式子的值．

解答 解：（1）∵（tanα-3）（sinα+cosα+3）=0，∴tanα=3，
∴$\frac{4sinα+2cosα}{5cosα+3sinα}$=$\frac{4tanα+2}{5+3tanα}$=$\frac{12+2}{5+9}$=1．
（2）$2+\frac{2}{3}{sin^2}α+\frac{1}{4}{cos^2}α$=$\frac{\frac{8}{3}{•sin}^{2}α+\frac{9}{4}{•cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{\frac{8}{3}{•tan}^{2}α+\frac{9}{4}}{{tan}^{2}α+1}$=$\frac{24+\frac{9}{4}}{9+1}$=$\frac{21}{8}$．

点评 本题主要考查同角三角函数的基本关系的应用，属于基础题．

练习册系列答案
相关题目
18．函数f（x）=3sin （2x-$\frac{π}{3}$） 的图象为C．
①图象C关于直线x=$\frac{11}{12}$π对称；
②函数f（x）在区间（-$\frac{π}{12}$，$\frac{5π}{12}$） 内是增函数；
③由y=3sin 2x的图象向右平移$\frac{π}{3}$个单位长度可以得到图象C．
以上三个论断中，正确论断的个数是（　　）
A．0个B．1个C．2个D．3个
19．已知f（x）=xn，若f′（-1）=3，则n的值为（　　）
A．3B．-4C．5D．-5
16．在△ABC中，内角A，B，C的对边分别为a，b，c，若c=2a，b=4，cosB=$\frac{1}{4}$．则边c的长度为（　　）
A．4B．2C．5D．6
3．已知集合P={x|x≤a}，Q={y|y=sinθ，θ∈R}．若P?Q，则实数a的取值范围是[1，+∞）．
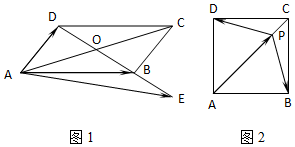13．（1）如图1，在平行四边形ABCD中，点E是对角线DB的延长线上一点，且OB=BE．记$\overrightarrow{AB}=\overrightarrow a\;，\;\overrightarrow{AD}=\overrightarrow b$，试用向量$\overrightarrow a\;，\;\overrightarrow b$表示$\overrightarrow{AE}$．
（2）若正方形ABCD边长为1，点P在线段AC上运动，求$\overrightarrow{AP}•（\overrightarrow{PB}+\overrightarrow{PD}）$的取值范围．
（3）设$\overrightarrow{OA}=\;\overrightarrow a，\;\overrightarrow{OB}=\overrightarrow b$，已知$\overrightarrow a•\overrightarrow b=|{\overrightarrow a-\overrightarrow b}|=2$，当△AOB的面积最大时，求∠AOB的大小．
20．若cos （$\frac{π}{3}$-α）=$\frac{3}{5}$，则cos（$\frac{2π}{3}$+α）=-$\frac{3}{5}$．
17．已知函数f（x）=x2-2elnx．（e为自然对数的底数）
（1）求函数f（x）的单调区间；
（2）求函数f（x）的图象在（1，f（1））处的切线方程．
18．设$α∈（0，\frac{π}{2}），β∈（0，\frac{π}{4}）$，且tanα=$\frac{cosβ+sinβ}{cosβ-sinβ}$，则下列正确的是（　　）
A．$2α-β=\frac{π}{4}$B．$2α+β=\frac{π}{4}$C．$α-β=\frac{π}{4}$D．$α+β=\frac{π}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网