题目内容
用反证法证明命题“设a，b为实数，则方程x3+ax+b=0至少有一个实根”时，要做的假设是（ ）
| A、方程x3+ax+b=0没有实根 |
| B、方程x3+ax+b=0至多有一个实根 |
| C、方程x3+ax+b=0至多有两个实根 |
| D、方程x3+ax+b=0恰好有两个实根 |
考点：反证法与放缩法
专题：函数的性质及应用
分析：直接利用命题的否定写出假设即可．
解答：
解：反证法证明问题时，反设实际是命题的否定，
∴用反证法证明命题“设a，b为实数，则方程x3+ax+b=0至少有一个实根”时，要做的假设是：方程x3+ax+b=0没有实根．
故选：A．
∴用反证法证明命题“设a，b为实数，则方程x3+ax+b=0至少有一个实根”时，要做的假设是：方程x3+ax+b=0没有实根．
故选：A．
点评：本题考查反证法证明问题的步骤，基本知识的考查．
练习册系列答案
相关题目
. |
| z |
. |
| z |
. |
| z |
| A、1+i | B、-1-i |
| C、-1+i | D、1-i |
若log4（3a+4b）=log2
，则a+b的最小值是（ ）
| ab |
A、6+2
| ||
B、7+2
| ||
C、6+4
| ||
D、7+4
|
下列函数为偶函数的是（ ）
| A、f（x）=x-1 |
| B、f（x）=x2+x |
| C、f（x）=2x-2-x |
| D、f（x）=2x+2-x |
设函数f（x），g（x）的定义域都为R，且f（x）是奇函数，g（x）是偶函数，则下列结论中正确的是（ ）
| A、f（x）g（x）是偶函数 |
| B、|f（x）|g（x）是奇函数 |
| C、f（x）|g（x）|是奇函数 |
| D、|f（x）g（x）|是奇函数 |
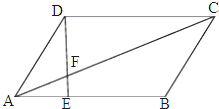如图，在平行四边形ABCD中，点E在AB上且EB=2AE，AC与DE交于点F，则