题目内容
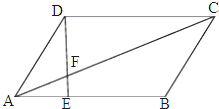如图，在平行四边形ABCD中，点E在AB上且EB=2AE，AC与DE交于点F，则| △CDF的面积 |
| △AEF的面积 |
考点：相似三角形的判定,三角形的面积公式
专题：解三角形
分析：利用ABCD是平行四边形，点E在AB上且EB=2AE，可得
=
，利用△CDF∽△AEF，可求
．
| CD |
| AE |
| 3 |
| 1 |
| △CDF的面积 |
| △AEF的面积 |
解答：
解：∵ABCD是平行四边形，点E在AB上且EB=2AE，
∴
=
，
∵ABCD是平行四边形，
∴AB∥CD，
∴△CDF∽△AEF，
∴
=（
）2=9．
故答案为：9．
∴
| CD |
| AE |
| 3 |
| 1 |
∵ABCD是平行四边形，
∴AB∥CD，
∴△CDF∽△AEF，
∴
| △CDF的面积 |
| △AEF的面积 |
| CD |
| AE |
故答案为：9．
点评：本题考查相似三角形的判定，考查三角形的面积比，属于基础题．
练习册系列答案
相关题目
用反证法证明命题“设a，b为实数，则方程x3+ax+b=0至少有一个实根”时，要做的假设是（ ）
| A、方程x3+ax+b=0没有实根 |
| B、方程x3+ax+b=0至多有一个实根 |
| C、方程x3+ax+b=0至多有两个实根 |
| D、方程x3+ax+b=0恰好有两个实根 |
如图，AB是⊙O的直径，P是AB延长线上的一点，过P作⊙O的切线，切点为C，AB=20，∠BAC=30°，AD⊥PC于D，则DE的长为