题目内容
在钝角三角形ABC中,若B=45°,a=
,则边长c的取值范围是( )
| 2 |
A、(1,
| ||
B、(0,1)∪(
| ||
| C、(1,2) | ||
| D、(0,1)∪(2,+∞) |
考点:余弦定理
专题:解三角形
分析:取临界状态并分类讨论,当A、C分别为直角时,可得c值,进而可得c的取值范围.
解答:
解:取临界状态并分类讨论:
当C为直角时,在直角三角形中,结合B=45°,a=
可得c=2,
要使△ABC钝角三角形,只需c>2即可;
当A为直角时,在直角三角形中,结合B=45°,a=
可得c=1,
要使△ABC钝角三角形,只需0<c<即可;
综上可得边长c的取值范围是:(0,1)∪(2,+∞)
故选:D
当C为直角时,在直角三角形中,结合B=45°,a=
| 2 |
要使△ABC钝角三角形,只需c>2即可;
当A为直角时,在直角三角形中,结合B=45°,a=
| 2 |
要使△ABC钝角三角形,只需0<c<即可;
综上可得边长c的取值范围是:(0,1)∪(2,+∞)
故选:D
点评:本题考查三角形的边长的取值范围,取临界状态并分类讨论是解决问题的关键,属中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
在平面直角坐标系中,不等式组
(a为常数)所表示的平面区域的面积是9,则实数a的值是( )
|
| A、1 | B、-5 |
| C、1或-5 | D、-1或5 |
两球的体积之比为8:1,则它们的表面积之比为( )
| A、8:1 | ||
| B、4:1 | ||
C、2
| ||
| D、2:1 |
某少数民族的刺绣有着悠久的历史,如图所示(1)(2)(3)(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.则f(5)等于( )


| A、39 | B、40 | C、41 | D、42 |
长方体的一个顶点上三条棱长分别是1、2、3,且它的8个顶点都在同一球面上,则这个球的表面积是( )
| A、7π | B、14π |
| C、28π | D、56π |
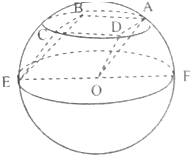 如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )
如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )A、4
| ||
B、4
| ||
C、2
| ||
D、2
|