题目内容
1.已知抛物线y2=8x的焦点为F,A、B为抛物线上两点,若$\overrightarrow{AF}=3\overrightarrow{FB}$,则△AOB的面积为( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{32\sqrt{3}}{3}$ | D. | $\frac{64\sqrt{3}}{3}$ |
分析 抛物线y2=8x的焦点为F(2,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,则|AB|=2|AE|,直线AB的倾斜角为60°,利用点斜式方程,求得直线AB的方程,与抛物线方程联立消去y,进而跟韦达定理求得x1+x2的值,则丨AB丨=x1+x2+p=$\frac{20}{3}$+4=$\frac{32}{3}$,利用点到直线的距离公式及三角形的面积公式即可求得△AOB的面积.
解答  解:抛物线y2=8x的焦点为F(2,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
解:抛物线y2=8x的焦点为F(2,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
过B做BE⊥AD,
由$\overrightarrow{AF}=3\overrightarrow{FB}$,则丨$\overrightarrow{AF}$丨=丨$\overrightarrow{FB}$丨,
∴|AB|=2|AE|,由抛物线的对称性,不妨设直线的斜率为正,
∴直线AB的倾斜角为60°,直线AB的方程为y=$\sqrt{3}$(x-2),
联立直线AB与抛物线的方程可得:$\left\{\begin{array}{l}{y=\sqrt{3}(x-2)}\\{{y}^{2}=8x}\end{array}\right.$,整理得:3x2-20x+12=0,
由韦达定理可知:x1+x2=$\frac{20}{3}$,则丨AB丨=x1+x2+p=$\frac{20}{3}$+4=$\frac{32}{3}$,
而原点到直线AB的距离为d=$\frac{丨2\sqrt{3}丨}{\sqrt{1+(\sqrt{3})^{2}}}$=$\sqrt{3}$,
则三角形△AOB的面积S=$\frac{1}{2}$•丨AB丨•d=$\frac{1}{2}$•$\frac{32}{3}$•$\sqrt{3}$=$\frac{16\sqrt{3}}{3}$,
∴当直线AB的倾斜角为120°时,同理可求S=$\frac{1}{2}$•丨AB丨•d=$\frac{1}{2}$•$\frac{32}{3}$•$\sqrt{3}$=$\frac{16\sqrt{3}}{3}$,.
故选B.
点评 本题考查抛物线的简单几何性质,考查抛物线的焦点弦公式,三角形面积公式及点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.

 发散思维新课堂系列答案
发散思维新课堂系列答案(1)求λ及k的值;
(2)设${b}_{n}=\frac{3}{2{S}_{n}}$,求数列{bn}的前n项和Tn.
| A. | $\frac{243π}{16}$ | B. | $\frac{81π}{16}$ | C. | $\frac{81π}{4}$ | D. | $\frac{27π}{4}$ |
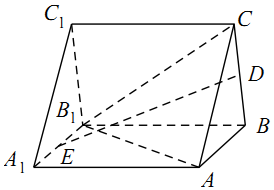 在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.