题目内容
13.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的体积为( )| A. | $\frac{243π}{16}$ | B. | $\frac{81π}{16}$ | C. | $\frac{81π}{4}$ | D. | $\frac{27π}{4}$ |
分析 正四棱锥P-ABCD的五个顶点在同一球面上,则其外接球的球心在它的高PO1上,记为O,求出AO1,OO1,解出球的半径,求出球的体积.
解答 解:正四棱锥P-ABCD的外接球的球心在它的高PO1上,
记为O,PO=AO=R,PO1=4,OO1=4-R,
在Rt△AO1O中,AO1=$\sqrt{2}$,由勾股定理R2=2+(4-R)2得R=$\frac{9}{4}$,
∴球的体积为$\frac{243}{16}π$.
故选A.
点评 本题考查球的表面积,球的内接体问题,解答关键是确定出球心的位置,利用直角三角形列方程式求解球的半径.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.已知抛物线y2=8x的焦点为F,A、B为抛物线上两点,若$\overrightarrow{AF}=3\overrightarrow{FB}$,则△AOB的面积为( )
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{32\sqrt{3}}{3}$ | D. | $\frac{64\sqrt{3}}{3}$ |
18.下列四个命题中,正确的是( )
| A. | 若x>1,则?y∈(-∞,1),xy≠1 | B. | 若x=sinθcosθ,则?θ∈(0,π),x≠$\frac{1}{2}$ | ||
| C. | 若x>1,则?y∈(-∞,1),xy=1 | D. | 若x=sinθcosθ,则?θ∈(0,π),x=1 |
3.若a<b<0,则下列不等式成立的是( )
| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
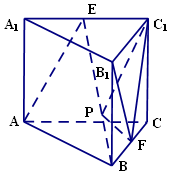 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.