题目内容
16.已知数列{an}的前n项和为Sn,a1=1,且3Sn=an+1-1.(1)求数列{an}的通项公式;
(2)设等差数列{bn}的前n项和为Tn,a2=b2,T4=1+S3,求$\frac{2{T}_{n}+48}{n}$的最小值.
分析 (1)利用a1=1,且3Sn=an+1-1.写出3Sn-1=an-1.两式相减得到4an=an+1,得到数列{an}是首项为1,公比为4的等比数列,得到通项公式;
(2)由a2=b2,T4=1+S3,得到关于b1=1,d=3,得到数列{bn}的前n项和为Tn,代入所求利用基本不等式求最小值.
解答 解:(1)∵3Sn=an+1-1①
∴当n>1时,3Sn-1=an-1.②,…(1分)
①-②得3(Sn-Sn-1)=3an=an+1-an,则4an=an+1,…(3分)
又a2=3a1+1=4=4a1,…(4分)
∴数列{an}是首项为1,公比为4的等比数列,
则an=4n-1…(6分)
(2)由(1)得a2=4,S3=21…(7分)
则$\left\{\begin{array}{l}{{b}_{2}=4}\\{{T}_{4}=2({b}_{1}+{b}_{4})=22}\end{array}\right.$,得b1=1,…(8分)
设数列{bn}的公差为d,则b1=1,d=3,…(9分)
∴Tn=$\frac{3}{2}{n}^{2}-\frac{1}{2}n$
∴$\frac{2{T}_{n}+48}{n}$=$\frac{3{n}^{2}-n+48}{n}=3n+\frac{48}{n}-1$≥2$\sqrt{3×48}$-1=23…(10分)
当且仅当n=4时取等号,…(11分)
∴$\frac{2{T}_{n}+48}{n}$的最小值为23…(12分)
点评 本题考查了数列{an}的通项与前n项和为Sn之间的关系求通项公式的方法以及等差数列的前n项和;体现了方程组的思想方法;属于中档题.

练习册系列答案
相关题目
6.若a∈{1,2},b∈{-2,-1,0,1,2},方程x2+ax+b=0的两根均为实数的概率( )
| A. | $\frac{3}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
7.设集合A={x|x2-4x+3≥0},B={x|2x-3≤0},则A∪B=( )
| A. | (-∞,1]∪[3,+∞) | B. | [1,3] | C. | $[{\frac{3}{2},3}]$ | D. | $({-∞,\frac{3}{2}}]∪[{3,+∞})$ |
11.已知命题p:若x<-3,则x2-2x-8>0,则下列叙述正确的是( )
| A. | 命题p的逆命题是:若x2-2x-8≤0,则x<-3 | |
| B. | 命题p的否命题是:若x≥-3,则x2-2x-8>0 | |
| C. | 命题p的否命题是:若x<-3,则x2-2x-8≤0 | |
| D. | 命题p的逆否命题是真命题 |
1.已知抛物线y2=8x的焦点为F,A、B为抛物线上两点,若$\overrightarrow{AF}=3\overrightarrow{FB}$,则△AOB的面积为( )
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{32\sqrt{3}}{3}$ | D. | $\frac{64\sqrt{3}}{3}$ |
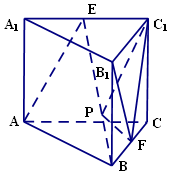 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.