题目内容
在(x+
)10的展开式中,x9项的系数为 .
| x |
考点:二项式定理
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于9,求得r的值,即可求得展开式中的x9项的系数.
解答:
解:(x+
)10的展开式的通项公式为Tr+1=
•x10-r•x
=
•x10-
,
令10-
=9,求得r=2,故x9项的系数为
=45,
故答案为:45.
| x |
| C | r 10 |
| r |
| 2 |
| C | r 10 |
| r |
| 2 |
令10-
| r |
| 2 |
| C | 2 10 |
故答案为:45.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
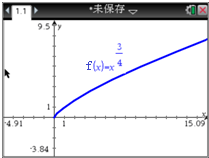 某同学利用TI-Nspire图形计算器作图作出幂函数f(x)=
某同学利用TI-Nspire图形计算器作图作出幂函数f(x)=