题目内容
20.设α、β为互不重合的平面,m、n为互不重合的直线,给出下列四个命题:①若m⊥α,n?α,则m⊥n;
②若m?α,n?α,m∥β,n∥β,则α∥β;
③若α⊥β,α∩β=m,n?α,m⊥n,则n⊥β;
④若m⊥α,α⊥β,m∥n,则n∥β.
其中所有正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,若m⊥α,n?α,则m⊥n,根据线面垂直的性质可判定;
②,若m?α,n?α,m∥β,n∥β,m、n不一定相交,则α∥β不一定成立;
③,若α⊥β,α∩β=m,n?α,m⊥n,则n⊥β,根据面面垂直的性质可判断;
④,若m⊥α,α⊥β,m∥n,则n∥β或n?β;
解答 解:设α、β为互不重合的平面,m、n为互不重合的直线,给出下列四个命题:
对于①,若m⊥α,n?α,则m⊥n,根据线面垂直的性质可判定①正确;
对于②,若m?α,n?α,m∥β,n∥β,∵m、n不一定相交,则α∥β不一定成立,故②错;
对于③,若α⊥β,α∩β=m,n?α,m⊥n,则n⊥β,根据面面垂直的性质可判定③正确;
对于④,若m⊥α,α⊥β,m∥n,则n∥β或n?β.故错;
故选:B.
点评 本题考查了空间线线、线面、面面位置关系的判定,属于中档题.

练习册系列答案
相关题目
10.如图是“二分法”求方程近似解的流程图,在①,②处应填写的内容分别是( )
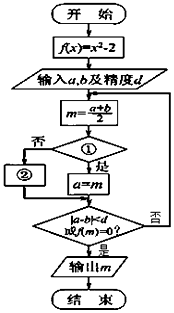

| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
11.设集合A={-1,0,1,2,3},B={x|x2-2x>0},则A∩(∁RB)=( )
| A. | {-1,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
8.复数$\frac{{(1-i{)^2}}}{3-i}$的值是( )
| A. | $-\frac{1}{4}+\frac{3}{4}i$ | B. | $\frac{1}{4}-\frac{3}{4}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
12.执行如图的程序框图,如果输入的x1=2000,x2=2,x3=5,则输出的b的值为( )


| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
10.随机变量X的取值为0,1,2,若P(X=0)=$\frac{1}{5}$,E(X)=1,则D(X)=( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{10}}{5}$ |
 如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数分别是18,23.
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数分别是18,23.