题目内容
10.随机变量X的取值为0,1,2,若P(X=0)=$\frac{1}{5}$,E(X)=1,则D(X)=( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{10}}{5}$ |
分析 设P(X=1)=p,P(X=2)=q,则由P(X=0)=$\frac{1}{5}$,E(X)=1,列出方程组,求出p=$\frac{3}{5}$,q=$\frac{1}{5}$,由此能求出D(X).
解答 解:设P(X=1)=p,P(X=2)=q,
∵E(X)=0×$\frac{1}{5}$+p+2q=1①,
又$\frac{1}{5}$+p+q=1,②
由①②得,p=$\frac{3}{5}$,q=$\frac{1}{5}$,
∴D(X)=$\frac{1}{5}$(0-1)2+$\frac{3}{5}(1-1)^{2}+\frac{1}{5}(2-1)^{2}$=$\frac{2}{5}$,
故选:B.
点评 本题考查离散型随机变量的方差的求法,考查离散型随机变量的分布列、数学期望的求法等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.共享单车进驻城市,绿色出行引领时尚,某市有统计数据显示,2016年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示,若将共享单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”,已知在“经常使用单车用户”中有$\frac{5}{6}$是“年轻人”.

(Ⅰ)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列2×2列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?
使用共享单车情况与年龄列联表
(Ⅱ)将频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量X,求X的分布列与期望.
(参考数据:
其中,K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d)

(Ⅰ)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列2×2列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?
使用共享单车情况与年龄列联表
| 年轻人 | 非年轻人 | 合计 | |
| 经常使用共享单车用户 | 120 | ||
| 不常使用共享单车用户 | 80 | ||
| 合计 | 160 | 40 | 200 |
(参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
5.已知关于x的方程|2x3-8x|+mx=4有且仅有2个实数根,则实数m的取值范围为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-1)∪(1,+∞) | C. | (-2,2) | D. | (-1,1) |
2.设(1+x)6=a0+a1x+a2x2+…+a6x6,其中x、ai∈R,i=0,1,…,6,则a1+a3+a5=( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
6.若某商品销售量y(件)与销售价格x(元/件)负相关,则其回归直线方程可能是( )
| A. | $\stackrel{∧}{y}$=-10x-100 | B. | $\stackrel{∧}{y}$=10x-100 | C. | $\stackrel{∧}{y}$=-10x+200 | D. | $\stackrel{∧}{y}$=10x-200 |
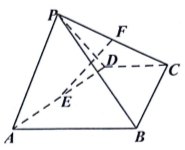 如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.
如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.