题目内容
已知p:log2(x+2)≤3,q:x2-2x+1-m2≤0(m>0),若p是q的充分不必要条件,则实数m的取值范围是 .
考点:必要条件、充分条件与充要条件的判断,其他不等式的解法
专题:不等式的解法及应用
分析:分别解不等式可得-2<x≤6和1-m≤x≤1+m,可得{x|-2<x≤6}?{x|1-m≤x≤1+m},解关于m的不等式组可得.
解答:
解:不等式log2(x+2)≤3可化为log2(x+2)≤log28,
由对数函数的单调性可得0<x+2≤8,解得-2<x≤6;
同理不等式x2-2x+1-m2≤0可化为[x-(1+m)][x-(1-m)]≤0,
∵m>0,∴1+m>1-m,∴1-m≤x≤1+m,
∵p是q的充分不必要条件,
∴{x|-2<x≤6}?{x|1-m≤x≤1+m},
∴6≤1+m,且1-m≤-2,解得m≥5
故答案为:m≥5.
由对数函数的单调性可得0<x+2≤8,解得-2<x≤6;
同理不等式x2-2x+1-m2≤0可化为[x-(1+m)][x-(1-m)]≤0,
∵m>0,∴1+m>1-m,∴1-m≤x≤1+m,
∵p是q的充分不必要条件,
∴{x|-2<x≤6}?{x|1-m≤x≤1+m},
∴6≤1+m,且1-m≤-2,解得m≥5
故答案为:m≥5.
点评:本题考查充要条件的判断,化为集合的包含关系是解决问题的关键,属基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
不等式|1-x|≥2的解集为( )
| A、{x|x≤-1或x≥3} |
| B、{x|x≥3} |
| C、{x|-1≤x≤3} |
| D、R |
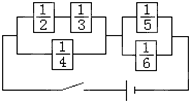 在如图所示的电路中,5只箱子表示保险匣,箱中所示数值表示通电时保险丝被切断的概率,若各保险匣之间互不影响,则当开关合上时,电路畅通的概率是( )
在如图所示的电路中,5只箱子表示保险匣,箱中所示数值表示通电时保险丝被切断的概率,若各保险匣之间互不影响,则当开关合上时,电路畅通的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
若一个样本的总偏差平方和为256,残差平方和为32,则回归平方和为( )
| A、224 | B、288 |
| C、320 | D、192 |