题目内容

若关于x的方程sin2x+cos2x=k在区间[0，
π
2
]上有实数解，则实数k的最大值为
 
．
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：先利用两角和公式对方程画家整理，进而根据x的范围确定k的范围．
解答： 解：k=sin2x+cos2x=
2
sin（2x+
π
4
），
∵x∈[0，
π
2
]，
∴2x+
π
4
∈[
π
4
，
5π
4
]，
∴-
2
2
≤sin（2x+
π
4
）≤1，
∴-1≤k≤
2
，
∴k的最大值为
2
，
故答案为：
2
点评：本题主要考查了三角函数恒等变换的应用．在解决三角函数范围问题，常结合三角函数图象来解决．
练习册系列答案
相关题目
已知数列{an}的通项an=n2+n，试问是否存在常数p，q，使等式
1
1+a1
+
1
2+a2
+…
1
n+an
=
pn2+qn
4(n+1)(n+2)
对一切自然数n都成立．若存在，求出p，q的值．并用数学归纳法证明，若不存在说明理由．
已知数列{an}的通项公式是an=n（n∈N*），数列{an}的前n项的和记为Sn，则
1
S1
+
1
S2
+
1
S3
+…+
1
S10
=
 
．
求“方程（
3
5
）x+（
4
5
）x=1的解”有如下解题思路：设f（x）=（
3
5
）x+（
4
5
）x，则f（x）在R上单调递减，且f（2）=1，所以原方程有唯一解x=2．类比上述解题思路求解：已知函数f（x）的定义域为R，对任意x∈R，有f'（x）＞3x2，且f（1）=2，则方程f（x）=x3+1的解集为
 
．
复数z在复平面内对应的点位于第二象限，且z•
.
z
+2i•
.
z
=8+ai（a∈R），则实数a的取值范围为
 
．
给出下列四个命题：
①若f（x+2）=f（2-x），则f（x）的图象关于x=2对称；
②若f（x+2）=f（2-x），则f（x）的图象关于y轴对称；
③函数y=f（2+x）与y=f（2-x）的图象关于x=2对称；
④函数y=f（2+x）与y=f（2-x）的图象关于y轴对称．正确命题的序号是
 
．
已知某人连续5次投掷飞镖的环数分别为9，10，8，10，8，则该组数据的方差为
 
．
若不等式kx2-6kx+k+8≥0对任意x∈R恒成立，则实数k的取值范围为
 
．
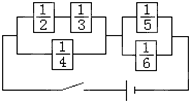在如图所示的电路中，5只箱子表示保险匣，箱中所示数值表示通电时保险丝被切断的概率，若各保险匣之间互不影响，则当开关合上时，电路畅通的概率是（　　）
A、
551
720
B、
29
144
C、
29
72
D、
29
36

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网