题目内容
已知Sn为等差数列{an}的前n项和，S1＜0，3S23+2S25=0，则Sn取最小值时，n的值是（ ）
| A、12 | B、13 | C、24 | D、26 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由3S23+2S25=0，求出d=-
a1，再利用等差数列的求和公式即可得出结论．
| 119 |
| 1359 |
解答：
解：∵3S23+2S25=0，
∴119a1+1359d=0，
∴d=-
a1，
∴Sn=na1+
d=
（2837n-119n2），
∴n=12时，Sn取最小值．
故选：A．
∴119a1+1359d=0，
∴d=-
| 119 |
| 1359 |
∴Sn=na1+
| n(n-1) |
| 2 |
| a1 |
| 2718 |
∴n=12时，Sn取最小值．
故选：A．
点评：本题考查等差数列的求和公式的运用，考查二次函数的性质，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
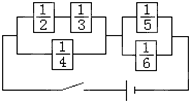在如图所示的电路中，5只箱子表示保险匣，箱中所示数值表示通电时保险丝被切断的概率，若各保险匣之间互不影响，则当开关合上时，电路畅通的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
掷一枚质地均匀的骰子n次，设出现k次点数为1的概率为Pn（k），若n=20，则当k为（ ）时Pn（k）取最大值．
| A、3 | B、4 | C、8 | D、10 |
已知函数f（x）的定义域为R，其导函数为f′（x），且f（x）+xf′（x）＜0恒成立，则三个数-f（-1），f（1），3f（3）的大小关系为（ ）
| A、-f（-1）＜f（1）＜3f（3） |
| B、f（1）＜-f（-1）＜3f（3） |
| C、-f（-1）＜3f（3）＜f（1） |
| D、3f（3）＜f（1）＜-f（-1） |
在△ABC中，角A，B，C的对边分别是a，b，c，若a=
，A=45°，B=60°，则b=（ ）
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若一个样本的总偏差平方和为256，残差平方和为32，则回归平方和为（ ）
| A、224 | B、288 |
| C、320 | D、192 |
函数f（x）=sinx+2xf′（
），f′（x）为f （x） 的导函数，令a=-
，b=log32，则下列关系正确的是（ ）
| π |
| 3 |
| 1 |
| 2 |
| A、f （a）＞f （b） |
| B、f （a）＜f （b） |
| C、f （a）=f （b） |
| D、f （|a|）＜f （b） |