题目内容
设定点A（0，1），动点P（x，y）的坐标满足条件
，则|PA|的最小值为（ ）
|
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式对应的平面区域，利用线性规划的知识，利用点到直线的距离公式即可得到结论．
解答：
解：作出不等式组对应的平面区域，
由图象可知点A到直线y=x的距离最小，
此时d=
=
=
，
即|PA|的最小值为
，
故选：A
由图象可知点A到直线y=x的距离最小，
此时d=
| |0-1| | ||
|
| 1 | ||
|
| ||
| 2 |
即|PA|的最小值为
| ||
| 2 |
故选：A
点评：本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．
练习册系列答案
阅读快车系列答案
相关题目
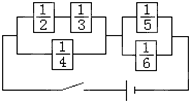在如图所示的电路中，5只箱子表示保险匣，箱中所示数值表示通电时保险丝被切断的概率，若各保险匣之间互不影响，则当开关合上时，电路畅通的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
若一个样本的总偏差平方和为256，残差平方和为32，则回归平方和为（ ）
| A、224 | B、288 |
| C、320 | D、192 |
已知扇形的圆心角为
弧度，半径为2，则扇形的面积为（ ）
| 2π |
| 3 |
A、
| ||
B、
| ||
| C、2π | ||
D、
|
已知△ABC的重心为O，AC=6．BC=7，AB=8，则
•
=（ ）
. |
| AO |
. |
| BC |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
曲线
ρ=4sin（θ+
）与曲线
的位置关系是（ ）
| 2 |
| π |
| 4 |
|
| A、相交过圆心 | B、相交不过圆心 |
| C、相切 | D、相离 |
函数f（x）=sinx+2xf′（
），f′（x）为f （x） 的导函数，令a=-
，b=log32，则下列关系正确的是（ ）
| π |
| 3 |
| 1 |
| 2 |
| A、f （a）＞f （b） |
| B、f （a）＜f （b） |
| C、f （a）=f （b） |
| D、f （|a|）＜f （b） |