题目内容
函数f（x）=ax2-ax+1（a≠0），如果f（-k）＜0，则f（k+1）的值是（ ）
| A、正数 | B、负数 | C、零 | D、无法确定 |
考点：二次函数的性质
专题：函数的性质及应用
分析：由-k，k+1关于对称轴x=
对称，得出f（k+1）=f（-k）＜0，问题得解．
| 1 |
| 2 |
解答：
解；∵对称轴x=-
=
，
且
=
，
∴-k，k+1关于x=
对称，
∴f（k+1）=f（-k）＜0，
故选：B．
| -a |
| 2a |
| 1 |
| 2 |
且
| k+1-k |
| 2 |
| 1 |
| 2 |
∴-k，k+1关于x=
| 1 |
| 2 |
∴f（k+1）=f（-k）＜0，
故选：B．
点评：本题考察了二次函数的性质问题，通过对称性解得，是一道基础题．
练习册系列答案
相关题目
在区间[-1，1]内随机取两个实数x，y，则满足y≥x-1的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，AC=6，BC=7，cosA=
，O是△ABC的内心，在△ABC内随机任取一点P，则取到满足条件
=x
+y
（0≤x≤1且0≤y≤1）时的点P的概率为（ ）
| 1 |
| 5 |
| OP |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={2a}，B={a，b），若A∩B={
}，则A∪B为（ ）
| 1 |
| 2 |
A、{
| ||
B、{-1，
| ||
C、{
| ||
D、{-1，
|
定义在实数集R函数f（x）满足f（x）+f（x+2）=0，且f（x-1）为奇函数，现有以下三种叙述：
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
| A、（2）（3） |
| B、（1）（2） |
| C、（1）（3） |
| D、（1）（2）（3） |
已知命题p：若非零实数a，b，则
＜
；命题q：对任意实数x∈（0，+∞），log
（x+1）＜0，则下列命题为真命题的是（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| A、p且q | B、p或￢q |
| C、￢p且q | D、p且￢q |
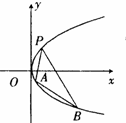如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），A（x1，y1），B（x2，y2）均在抛物线上．