题目内容
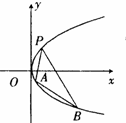 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.(1)求该抛物线方程;
(2)若AB的中点坐标为(1,-1),求直线AB方程.
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意设出抛物线方程,代入P点坐标求p,则抛物线方程可求;
(2)把A,B的坐标代入抛物线方程,作差后结合AB的中点坐标求出AB所在直线的斜率,由点斜式得AB所在直线方程.
(2)把A,B的坐标代入抛物线方程,作差后结合AB的中点坐标求出AB所在直线的斜率,由点斜式得AB所在直线方程.
解答:
解:(1)由题意可设抛物线方程为y2=2px(p>0),
∵P(1,2)在抛物线上,
∴22=2p,即p=2.
∴抛物线方程为:y2=4x;
(2)∵A(x1,y1),B(x2,y2)在抛物线上,
∴y12=4x1,y22=4x2.
两式作差得:(y1-y2)(y1+y2)=4(x1-x2),
=
.
又AB的中点坐标为(1,-1),
∴y1+y2=-2,
则kAB=
=
=-2.
∴直线AB方程为y+1=-2(x-1),
即2x+y-1=0.
∵P(1,2)在抛物线上,
∴22=2p,即p=2.
∴抛物线方程为:y2=4x;
(2)∵A(x1,y1),B(x2,y2)在抛物线上,
∴y12=4x1,y22=4x2.
两式作差得:(y1-y2)(y1+y2)=4(x1-x2),
| y1-y2 |
| x1-x2 |
| 4 |
| y1+y2 |
又AB的中点坐标为(1,-1),
∴y1+y2=-2,
则kAB=
| y1-y2 |
| x1-x2 |
| 4 |
| -2 |
∴直线AB方程为y+1=-2(x-1),
即2x+y-1=0.
点评:本题考查了抛物线方程的求法,训练了利用“点差法”求直线的斜率,涉及中点弦问题常用此法解决,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数
=( )
| 1+3i |
| 1-i |
| A、2+i | B、2-i |
| C、-1+2i | D、-1-2i |
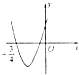 如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
函数f(x)=ax2-ax+1(a≠0),如果f(-k)<0,则f(k+1)的值是( )
| A、正数 | B、负数 | C、零 | D、无法确定 |