题目内容
已知在直角坐标平面上,向量
=(-3,2λ),
=(-3λ,2),定点A(3,0),其中0<λ<1.一自点A发出的光线以
为方向向量射到y轴的B点处,并被y轴反射,其反射光线与自点A以
为方向向量的光线相交于点P.
(1)求点P的轨迹方程;
(2)问A、B、P、O四点能否共圆(O为坐标原点),并说明理由.
| a |
| b |
| a |
| b |
(1)求点P的轨迹方程;
(2)问A、B、P、O四点能否共圆(O为坐标原点),并说明理由.
考点:轨迹方程,平面向量数量积的运算
专题:综合题
分析:(1)求出直线AB方程,可得B的坐标,P点关于y轴的对称点为P'(-x,y),则P'在直线AB上,可得方程y=-
(-x-3);直线AP的斜率为-
,可得方程y=-
(x-3),联立消去λ可得到x和y的关系,即可求出点P的轨迹方程;
(2)四点共圆,由于OA⊥OB,那么要算下PB和PA是否垂直,如果成立,则结论成立.
| 2λ |
| 3 |
| 2 |
| 3λ |
| 2 |
| 3λ |
(2)四点共圆,由于OA⊥OB,那么要算下PB和PA是否垂直,如果成立,则结论成立.
解答:
解:(1)设P(x,y),则直线AB的斜率为-
,则直线AB方程为y=-
(x-3),
则可得到B点(0,2λ),
P点关于y轴的对称点为P'(-x,y),则P'在直线AB上,可得方程y=-
(-x-3);
直线AP的斜率为-
,可得方程y=-
(x-3),
联立消去λ可得到x和y的关系
+
=1,即点P的轨迹方程为
+
=1;
(2)四点共圆,由于OA⊥OB,那么要算下PB和PA是否垂直,如果成立,则结论成立.
kPA•kPB=
•
≠-1,∴A、B、P、O四点不共圆.
| 2λ |
| 3 |
| 2λ |
| 3 |
则可得到B点(0,2λ),
P点关于y轴的对称点为P'(-x,y),则P'在直线AB上,可得方程y=-
| 2λ |
| 3 |
直线AP的斜率为-
| 2 |
| 3λ |
| 2 |
| 3λ |
联立消去λ可得到x和y的关系
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| 9 |
| y2 |
| 4 |
(2)四点共圆,由于OA⊥OB,那么要算下PB和PA是否垂直,如果成立,则结论成立.
kPA•kPB=
| y |
| x-3 |
| y-2λ |
| x |
点评:本题考查轨迹方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆C:x2+y2-2x-2y=0,且圆中过点(2,3)的最短弦为AB,则直线AB在x轴上的截距为( )
| A、-6 | B、2 | C、4 | D、8 |
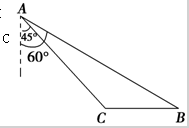 如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(