题目内容

19．已知x，y的取值如表：
x0134
ya4.34.86.7
若x，y具有线性相关关系，且回归方程为$\hat y=0.95x+2.6$，则a=2.2．

分析 求出样本中心点，代入$\hat y=0.95x+2.6$，可得a的值．

解答 解：由题意，$\overline{x}$=$\frac{1}{4}$（0+1+3+4）=2，$\overline{y}$=$\frac{1}{4}$（a+4.3+4.8+6.7）=$\frac{1}{4}$（15.8+a），
代入$\hat y=0.95x+2.6$可得$\frac{1}{4}$（15.8+a）=0.95×2+2.6，
∴a=2.2．
故答案为：2.2．

点评 本题考查回归直线方程的求法，是统计中的一个重要知识点，由公式得到样本中心点在回归直线上是关键．

练习册系列答案
相关题目
9．已知F1，F2分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，椭圆C上存在点P使∠F1PF2为钝角，则椭圆C的离心率的取值范围是（　　）
A．（$\frac{\sqrt{2}}{2}$，1）B．（$\frac{1}{2}$，1）C．（0，$\frac{\sqrt{2}}{2}$）D．（0，$\frac{1}{2}$）
10．将函数$y=sin（{x-\frac{π}{3}}）$的图象上每点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变），得到函数y=f（x）的图象．
（1）求函数f（x）的解析式及其图象的对称轴方程；
（2）在△ABC中，内角A，B，C的对边分别为a，b，c．若$f（A）=\frac{{\sqrt{3}}}{2}，a=2，b=\frac{{2\sqrt{3}}}{3}$，求sinB的值．
7．已知命题甲是“{x|$\frac{{x}^{2}+x}{x-1}$≥0}”，命题乙是“{x|log3（2x+1）≤0}”，则甲是乙的必要不充分条件．（从充分不必要、必要不充分、充要、既不充分也不必要中选填）
14．已知函数f（x）=lnx+$\frac{a}{x}（{a＞0}）$．
（Ⅰ） 若函数f（x）有零点，求实数a的取值范围；
（Ⅱ） 证明：当a≥$\frac{2}{e}$，b＞1时，f（lnb）＞$\frac{1}{b}$．
4．已知函数f（x）=lnx+bx-c，f（x）在点（1，f（1））处的切线方程为x+y+4=0．
（1）求f（x）的解析式；
（2）求f（x）的单调区间；
（3）若函数f（x）在定义域内恒有f（x）≥2lnx+kx成立，求k的取值范围．
4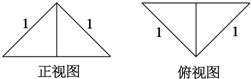．把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A-BCD的正视图与俯视图如图所示，则其侧视图的面积为$\frac{1}{4}$，二面角B-AC-D的余弦值为$-\frac{1}{3}$．
1．由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理叫（　　）
A．合情推理B．演绎推理C．类比推理D．归纳推理
2．执行下面的程度框图，若输出的值为-5，则判断框中可以填（　　）
A．z＞10B．z≤10C．z＞20D．z≤20

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网