��Ŀ����
2��ij���Ϲ�˾��Ƹ��һ��Ա�����ֶ������һ����ԣ��Ա�ȷ�����ʼ��𣮹�˾�������ֲ�ͬ�����Ϲ�8��������ɫ��ȫ��ͬ����������4��ΪA���ϣ�����4��ΪB���ϣ���˾Ҫ���Ա��һһƷ����8��������ѡ��4��A���ϣ���4����ѡ�ԣ����¹��ʶ�Ϊ3500Ԫ����4��ѡ��3�������¹��ʶ�Ϊ2800Ԫ�������¹��ʶ�Ϊ2100Ԫ����X��ʾ����ѡ��A���ϵı�����������˶�A��B��������û�м�����������1����X�ķֲ��У�
��2�����Ա���¹��ʱ���Ϊ2100Ԫ�ĸ��ʣ�
���� ��1��������֪��X�����п���ȡֵΪ0��1��2��3��4��
�ֱ�����Ӧ�ĸ���ֵ��д��X�ķֲ��У�
��2�����Ա���¹��ʱ���Ϊ2100ԪΪ�¼�M���ó�P��M��=P��X��2����
����������¼��ĸ��ʹ�ʽ���㼴�ɣ�
��� �⣺��1��������֪��X�����п���ȡֵΪ��0��1��2��3��4������2�֣�
��$P��X=i��=\frac{{C_4^iC_4^{4-i}}}{C_8^4}��i=0��1��2��3��4��$��
��$P��X=0��=\frac{C_4^0C_4^4}{C_8^4}=\frac{1}{70}$��
$P��X=1��=\frac{C_4^1C_4^3}{C_8^4}=\frac{16}{70}$��
$P��X=2��=\frac{C_4^2C_4^2}{C_8^4}=\frac{36}{70}$��
$P��X=3��=\frac{C_4^3C_4^1}{C_8^4}=\frac{16}{70}$��
$P��X=4��=\frac{C_4^4C_4^0}{C_8^4}=\frac{1}{70}$������7�֣�
���ԣ�X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{70}$ | $\frac{16}{70}$ | $\frac{36}{70}$ | $\frac{16}{70}$ | $\frac{1}{70}$ |
��2�����Ա���¹��ʱ���Ϊ2100ԪΪ�¼�M����
P��M��=P��X��2��
=P��X=0��+P��X=1��+P��X=2��
=$\frac{1}{70}$+$\frac{16}{70}$+$\frac{36}{70}$=$\frac{53}{70}$������13�֣�
���Դ�Ա���¹��ʱ���Ϊ2100Ԫ�ĸ���Ϊ$\frac{53}{70}$������14�֣�
���� ���⿼������ɢ������¼��ĸ�����ֲ��еļ������⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
�����Ŀ
19����$a=\int_0^��{sinxdx}$����${��a\sqrt{x}+\frac{1}{x}��^6}$չ��ʽ�ij�����Ϊ��������
| A�� | -20 | B�� | 20 | C�� | -160 | D�� | 240 |
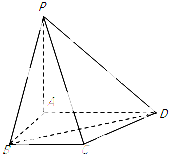 ��ͼ������P-ABCD�У�PA��ƽ��ABCD��AD��BC��AB��AD��BC=$\frac{2\sqrt{3}}{3}$��AB=1��BD=PA=2��������A-PD-C������ֵ��
��ͼ������P-ABCD�У�PA��ƽ��ABCD��AD��BC��AB��AD��BC=$\frac{2\sqrt{3}}{3}$��AB=1��BD=PA=2��������A-PD-C������ֵ��