题目内容
已知Sn为等差数列{an}的前n项和,若a1=-2013,
-
=6,则S2014=( )
| S2010 |
| 2010 |
| S2004 |
| 2004 |
| A、2013 | B、2014 |
| C、0 | D、2 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:利用等差数列的前n项和公式表示出S2010和S2004,代入已知的等式中,根据等差数列的性质列出关于公差d的方程,求出方程的解可求出公差d的值,再由首项的值,利用等差数列的前n项和公式即可求出S2014的值.
解答:
解:设数列{an}的公差为d,Sn=na1+
,
则
=
+
=a1+
,
=a1+
=a1+
,
∴
-
=3d=6,解得d=2
S2014=-2013×2014+
×2=0.
故选:C.
| n(n-1)d |
| 2 |
则
| S2010 |
| 2010 |
| a | 1 |
| (2010-1)d |
| 2 |
| 2009d |
| 2 |
| S2004 |
| 2004 |
| (2004-1)d |
| 2 |
| 2003d |
| 2 |
∴
| S2010 |
| 2010 |
| S2004 |
| 2004 |
S2014=-2013×2014+
| 2014×2013 |
| 2 |
故选:C.
点评:此题考查了等差数列的前n项和公式,以及等差数列的性质,其中求出公差d的值,是解题的关键.

练习册系列答案
相关题目
已知数列1,a1,a2,9成等差数列,1,b1,b2,b3,9成等比数列,则
=( )
| a1+a2 |
| b2 |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、±
|
不等式-x2+x+2≥0的解集是( )
| A、[-1,2] |
| B、(-∞,-1]∪[2,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
已知集合A={x|x2-x<0},B={x|x2+(1-a)x-a<0},则“a>1”是“A∩B≠∅”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若
=
,则cosα+sinα=( )
| cos2α | ||
cos(
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={-1,0,1,2},B={x|ln(x-1)=0},则A∩B=( )
| A、{-1} | B、{0} |
| C、{1} | D、{2} |
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
)的部分图象如图所示,则( )
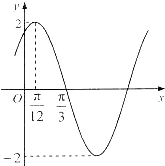
| π |
| 2 |

A、ω=2,φ=
| ||||
B、ω=
| ||||
C、ω=2,φ=
| ||||
D、ω=
|