题目内容
已知集合A={-1，0，1，2}，B={x|ln（x-1）=0}，则A∩B=（ ）
| A、{-1} | B、{0} |
| C、{1} | D、{2} |
考点：交集及其运算
专题：集合
分析：求得集合B，根据交集的定义计算．
解答：
解：由ln（x-1）=0得x=2，
∴B={2}，∴A∩B={2}．
故选：D．
∴B={2}，∴A∩B={2}．
故选：D．
点评：本题考查了交集的定义及运算，熟练掌握交集的定义是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
若a＞b，则下列不等式成立的是（ ）
| A、ac＞bc | ||||
| B、ac2＞bc2 | ||||
C、
| ||||
| D、a+c＞b+c |
已知向量
=（2，3），
=（x，-6），且
∥
，则x=（ ）
| a |
| b |
| a |
| b |
| A、4 | B、-4 | C、9 | D、-9 |
已知Sn为等差数列{an}的前n项和，若a1=-2013，
-
=6，则S2014=（ ）
| S2010 |
| 2010 |
| S2004 |
| 2004 |
| A、2013 | B、2014 |
| C、0 | D、2 |
已知实数x，y满足
=x-y，若y≥3，则x的最小值为（ ）
| x |
| y |
| A、2 | ||
| B、4 | ||
C、
| ||
| D、5 |
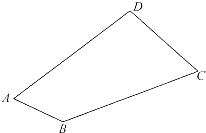如图，在四边形ABCD中，若∠A=∠C=60°，AD=BC=2，且AB≠CD，则四边形ABCD的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、与点B的位置有关 |
在等比数列{an}中，a3=
，其前三项的和S3=
，则数列{an}的公比等于（ ）
| 3 |
| 2 |
| 9 |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|