题目内容
已知数列{an}满足a1=0,an+1=
,则a31是( )
an-
| ||
|
| A、0 | ||||
B、-
| ||||
C、
| ||||
D、
|
考点:数列递推式
专题:转化思想,等差数列与等比数列
分析:本题利用条件依次求出数列的各项a1,a2,a3,a4,…,从而发现数列的周期性规律,得出本题结论.求出其中的某一项a31,得出本题结论.
解答:
解:∵数列{an}满足a1=0,an+1=
,
∴a1=
=-
,
a2=
=
,
a3=
=0,
a4=
=-
,
…
∴an=an+3,n∈N.
∴a31=a1=0.
故选A.
an-
| ||
|
∴a1=
0-
| ||
0×
|
| 3 |
a2=
-
| ||||
|
| 3 |
a3=
| ||||
|
a4=
0-
| ||
0×
|
| 3 |
…
∴an=an+3,n∈N.
∴a31=a1=0.
故选A.
点评:本题考查了数列的归纳法,利用得到的规律解决问题,本题有一定的思维难度,属于中档题.

练习册系列答案
相关题目
已知sin(π+α)=-
,则tan(α-7π)的值等于( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、±
| ||||
D、-
|
f(x)为定义在实数上的可导函数,且f(x)<f′(x)对任意的x∈R都成立,则( )
| A、f(1)>ef(0),f(2013)>e2013f(0) |
| B、f(1)<ef(0),f(2013)>e2013f(0) |
| C、f(1)>ef(0),f(2013)<e2013f(0) |
| D、f(1)<ef(0),f(2013)<e2013f(0) |
抽屉中有10只外观一样的手表,其中有3只是坏的,现从抽屈中随机地抽取4只,那么
等于( )
| 1 |
| 6 |
| A、恰有1只是坏的概率 |
| B、恰有2只是坏的概率 |
| C、恰有4只是好的概率 |
| D、至多2只是坏的概率 |
已知,A(-3,1)、B(2,-4),则直线AB上方向向量
的坐标是( )
| AB |
| A、(-5,5) |
| B、(-1,-3) |
| C、(5,-5) |
| D、(-3,-1) |
函数y=
的值域是( )
| 2x+1 |
| x-3 |
| A、(-∞,3)∪(3,+∞) |
| B、(-∞,2)∪(2,+∞) |
| C、R |
| D、(-∞,2)∪(3,+∞) |
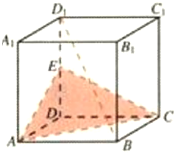 如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,
如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,