题目内容
已知函数f(x)=(x-a)2ex,g(x)=x3-x2-3,其中a∈R.
(1)当a=0时,求曲线y=f(x)在点P(1,f(1))处的切线方程;
(2)若存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,求实数M的最大值;
(3)若对任意的s,t∈[0,2],都有f(s)≥g(t),求实数a的取值范围.
(1)当a=0时,求曲线y=f(x)在点P(1,f(1))处的切线方程;
(2)若存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,求实数M的最大值;
(3)若对任意的s,t∈[0,2],都有f(s)≥g(t),求实数a的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的概念及应用,导数的综合应用
分析:(1)在P(1,f(1))处的切线方程,说明P是切点,先将点P代入f(x)得解析式求出f(2),求出切点坐标,再求出原函数导数,求出P处的导数,则利用点斜式可求出切线方程;
(2)首先g(x1)与g(x2)是两个函数,因为存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,所以要求M的最大值,只需求g(x1)max-g(x2)min即可,实际上就是求函数y=g(x)在区间[0,2]上的最大值、最小值,借助单调性容易解决;
(3)这是一个恒成立问题,且是两个函数,所以只需f(s)min≥g(t)max即可,由此构造关于a的不等式(组)即可.
(2)首先g(x1)与g(x2)是两个函数,因为存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,所以要求M的最大值,只需求g(x1)max-g(x2)min即可,实际上就是求函数y=g(x)在区间[0,2]上的最大值、最小值,借助单调性容易解决;
(3)这是一个恒成立问题,且是两个函数,所以只需f(s)min≥g(t)max即可,由此构造关于a的不等式(组)即可.
解答:
解:(1)当a=0时,f(x)=x2ex,f'(x)=ex(x2+2x),f(1)=e,f'(x)=3e,
所以所求切线方程为y-e=3e(x-1),即y=3ex-2e.
(2)g′(x)=3x(x-
),x∈[0,2].令g'(x)=0,得x1=0,x2=
.
当x变化时,g'(x)与g(x)的变化情况如下:
所以[g(x)]max=max{g(0),g(2)}=g(2)=1,[g(x)]min=g(
)=-
.
因为存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,
所以M≤[g(x)]max-[g(x)]min=
.所以实数M的最大值为
.
(3)由(2)知,在[0,2]上,[g(x)]max=g(2)=1,所以f(x)min≥1,f'(x)=ex(x-a)(x-a+2).
(ⅰ)当a≤0或a≥4时,在[0,2]上,f'(x)≥0,f(x)是单调增函数.
所以f(x)min=f(0)=a2≥1,解得a≤-1或a≥1.
所以a≤-1或a≥4.
(ⅱ)当0<a<2时,在[0,a]上,f'(x)≤0,f(x)是单调减函数;在[a,2]上,f'(x)≥0,f(x)是单调增函数.
所以f(x)min=f(a)=0≥1,不成立.
(ⅲ)当2<a<4时,在[0,a]上,f'(x)≥0,f(x)是单调增函数;在[a,2]上,f'(x)≤0,f(x)是单调减函数.
所以f(0)=a2≥1且 f(2)=(2-a)2e2≥1,又2<a<4,可得2+
≤a<4.
(ⅳ)当a=2时,在[0,2]上,f'(x)≤0,f(x)是单调减函数.f(x)min=f(2)=(2-a)2e2=0≥1,不成立.
综上,实数a的取值范围是(-∞,-1]∪[2+
,+∞).
所以所求切线方程为y-e=3e(x-1),即y=3ex-2e.
(2)g′(x)=3x(x-
| 2 |
| 3 |
| 2 |
| 3 |
当x变化时,g'(x)与g(x)的变化情况如下:
| x | 0 | (0,
|
| (
| 2 | ||||||
| g'(x) | - | 0 | + | ||||||||
| g(x) | -3 | ↘ | 极小值 | ↗ | 1 |
| 2 |
| 3 |
| 85 |
| 27 |
因为存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,
所以M≤[g(x)]max-[g(x)]min=
| 112 |
| 27 |
| 112 |
| 27 |
(3)由(2)知,在[0,2]上,[g(x)]max=g(2)=1,所以f(x)min≥1,f'(x)=ex(x-a)(x-a+2).
(ⅰ)当a≤0或a≥4时,在[0,2]上,f'(x)≥0,f(x)是单调增函数.
所以f(x)min=f(0)=a2≥1,解得a≤-1或a≥1.
所以a≤-1或a≥4.
(ⅱ)当0<a<2时,在[0,a]上,f'(x)≤0,f(x)是单调减函数;在[a,2]上,f'(x)≥0,f(x)是单调增函数.
所以f(x)min=f(a)=0≥1,不成立.
(ⅲ)当2<a<4时,在[0,a]上,f'(x)≥0,f(x)是单调增函数;在[a,2]上,f'(x)≤0,f(x)是单调减函数.
所以f(0)=a2≥1且 f(2)=(2-a)2e2≥1,又2<a<4,可得2+
| 1 |
| e |
(ⅳ)当a=2时,在[0,2]上,f'(x)≤0,f(x)是单调减函数.f(x)min=f(2)=(2-a)2e2=0≥1,不成立.
综上,实数a的取值范围是(-∞,-1]∪[2+
| 1 |
| e |
点评:本题主要是研究不等式有解、恒成立的问题,一般转化为函数的最值问题,但此例第(2)(3)问涉及到两个函数,此时要注意分别研究它们的最值,再构造不等式(组)求解.其中第(3)问涉及的讨论主要是讨论极值点与区间的关系,由此来确定函数在区间[0,2]上的单调性,进而求解.

练习册系列答案
相关题目
抽屉中有10只外观一样的手表,其中有3只是坏的,现从抽屈中随机地抽取4只,那么
等于( )
| 1 |
| 6 |
| A、恰有1只是坏的概率 |
| B、恰有2只是坏的概率 |
| C、恰有4只是好的概率 |
| D、至多2只是坏的概率 |
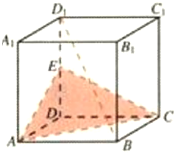 如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,
如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,