题目内容
17.已知曲线C1的极坐标方程为ρcosθ-ρsinθ+2=0,曲线C2的参数方程为$\left\{\begin{array}{l}x=cosα\\ y=2sinα\end{array}\right.$(α为参数),将曲线C2上的所有点的横坐标变为原来的3倍,纵坐标变为原来的$\frac{3}{2}$倍,得到曲线C3.(1)写出曲线C1的参数方程和曲线C3的普通方程;
(2)已知点P(0,2),曲线C1与曲线C3相交于A,B,求|PA|+|PB|.
分析 (1)由x=ρcosθ,y=ρsinθ化直线方程为普通方程,写出过P(0,2)的直线参数方程,由题意可得$\left\{\begin{array}{l}{x=3cosα}\\{y=3sinα}\end{array}\right.$,运用同角平方关系化为普通方程;
(2)将直线的参数方程代入曲线C3的普通方程,可得t的方程,运用韦达定理和参数的几何意义,即可得到所求和.
解答 解:(1)曲线C1的极坐标方程为ρcosθ-ρsinθ+2=0,
可得普通方程为x-y+2=0,
则C1的参数方程为$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),
由曲线C2的参数方程为$\left\{\begin{array}{l}x=cosα\\ y=2sinα\end{array}\right.$(α为参数),
可得$\left\{\begin{array}{l}{x=3cosα}\\{y=3sinα}\end{array}\right.$,
即有C3的普通方程为x2+y2=9.…(5分)
(2)C1的标准参数方程为$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),
与C3联立可得t2+2$\sqrt{2}$t-5=0,
令|PA|=|t1|,|PB|=|t2|,由韦达定理,
则有t1+t2=-2$\sqrt{2}$,t1t2=-5,
则|PA|+|PB|=|t1|+|t2|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$
=$\sqrt{8-4×(-5)}$=2$\sqrt{7}$…(10分)
点评 本题考查极坐标方程、参数方程和普通方程的互化,考查直线的参数方程的运用,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案 | 1014年(1-12月) | 1015年(1-12月) | 1016年(1-11月) |
| 接单量(单) | 14463272 | 40125125 | 50331996 |
| 油费(元) | 214301962 | 591305364 | 653214963 |
| 平均每单油费t(元) | 14.82 | 14.49 | |
| 平均每单里程k(公里) | 15 | 15 | |
| 每公里油耗a(元) | 0.7 | 0.7 | 0.7 |
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里)
 某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).(1)根据茎叶图中的数据完成2×2列联表,并判断能否有95%的把握认为孩子的幸福感强与是否是留守儿童有关?
| 幸福感强 | 幸福感弱 | 总计 | |
| 留守儿童 | 6 | 9 | 15 |
| 非留守儿童 | 18 | 7 | 25 |
| 总计 | 24 | 16 | 40 |
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
附表:
| P(K2≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
| A. | [$\sqrt{3}$-1,$\sqrt{3}$+1] | B. | [1,3] | C. | [$\sqrt{3}$-1,2] | D. | [1,$\sqrt{3}$+1] |
| A. | $(2k-\frac{1}{4},2k+\frac{1}{4}),k∈Z$ | B. | $(2k+\frac{1}{2},2k+\frac{5}{2}),k∈Z$ | ||
| C. | $(4k-\frac{1}{4},4k+\frac{1}{4}),k∈Z$ | D. | $(4k+\frac{1}{4},4k+\frac{15}{4}),k∈Z$ |
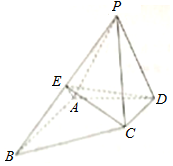 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点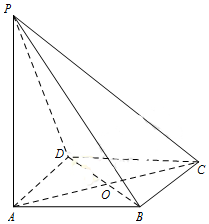 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.