题目内容
12. 某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).(1)根据茎叶图中的数据完成2×2列联表,并判断能否有95%的把握认为孩子的幸福感强与是否是留守儿童有关?
| 幸福感强 | 幸福感弱 | 总计 | |
| 留守儿童 | 6 | 9 | 15 |
| 非留守儿童 | 18 | 7 | 25 |
| 总计 | 24 | 16 | 40 |
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
附表:
| P(K2≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
分析 (1)根据题意,填写2×2列联表,计算观测值,对照临界值表得出结论;
(2)按分层抽样方法抽出幸福感强的孩子,利用列举法得出基本事件数,求出对应的概率值.
解答 解:(1)根据题意,填写2×2列联表如下:
| 幸福感强 | 幸福感弱 | 总计 | |
| 留守儿童 | 6 | 9 | 15 |
| 非留守儿童 | 18 | 7 | 25 |
| 总计 | 24 | 16 | 40 |
对照临界值表得,有95%的把握认为孩子的幸福感强与是否留守儿童有关;…(6分)
(2)按分层抽样的方法可抽出幸福感强的孩子2人,记作:a1,a2;
幸福感弱的孩子3人,记作:b1,b2,b3;
“抽取2人”包含的基本事件有(a1,a2),(a1,b1),(a1,b2),(a1,b3),
(a2,b1),(a2,b2),(a2,b3),
(b1,b2),(b1,b3),(b2,b3)共10个;…(8分)
事件A:“恰有一人幸福感强”包含的基本事件有
(a1,b1),(a1,b2),(a1,b3),
(a2,b1),(a2,b2),(a2,b3)共6个;…(10分)
故所求的概率为$P(A)=\frac{6}{10}=\frac{3}{5}$.…(12分)
点评 本题考查了对立性检验与分层抽样方法和列举法求古典概型的概率问题,是综合性题目.

练习册系列答案
相关题目
2.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
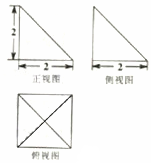

| A. | 4π | B. | 12π | C. | 48π | D. | 6$\sqrt{3}$π |
3.设a=log310,b=log37,则3a-b=( )
| A. | $\frac{10}{49}$ | B. | $\frac{49}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{10}{7}$ |
20.设x,y∈R,则“|x|+|y|>1”的一个充分条件是( )
| A. | |x|≥1 | B. | |x+y|≥1 | C. | y≤-2 | D. | $|x|≥\frac{1}{2}$且$|y|≥\frac{1}{2}$ |
2.若集合A={x|x2-3x-10<0},集合B={x|-3<x<4},全集为R,则A∩(∁RB)等于( )
| A. | (-2,4) | B. | [4,5) | C. | (-3,-2) | D. | (2,4) |
 如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.
如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.