题目内容
9.函数y=cos 2x+2sin x的最大值为( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 利用二倍角公式化简函数y,根据正弦函数的有界性与二次函数的图象与性质即可求出函数y的最大值.
解答 解:y=cos 2x+2sin x
=-2sin2x+2sin x+1,
设t=sin x,则-1≤t≤1,
所以原函数可以化为
y=-2t2+2t+1
=-2${(t-\frac{1}{2})}^{2}$+$\frac{3}{2}$,
所以当t=$\frac{1}{2}$时,函数y取得最大值为$\frac{3}{2}$.
故选:C.
点评 本题考查了二倍角公式与正弦函数和二次函数的应用问题,是基础题目.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
19.要得到函数$y=cos({2x-\frac{π}{3}})$的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
20.设x,y∈R,则“|x|+|y|>1”的一个充分条件是( )
| A. | |x|≥1 | B. | |x+y|≥1 | C. | y≤-2 | D. | $|x|≥\frac{1}{2}$且$|y|≥\frac{1}{2}$ |
14.复数$z=\frac{i}{1-i}$的共轭复数的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
 如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.
如图所示的多面体ABCDE中,已知ABCD是边长为2的正方形,平面ABCD⊥平面ABE,∠AEB=90°,AE=BE.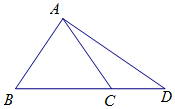 已知△ABC是等边三角形,D在BC的延长线上,且CD=2,${S_{△ABD}}=6\sqrt{3}$.
已知△ABC是等边三角形,D在BC的延长线上,且CD=2,${S_{△ABD}}=6\sqrt{3}$.