题目内容
若不等式ax2+bx+2>0的解集为{x|-
<x<
},则a+b= .
| 1 |
| 2 |
| 1 |
| 3 |
考点:一元二次不等式的应用
专题:计算题,不等式的解法及应用
分析:利用不等式的解集与方程解的关系,结合韦达定理,确定a,b的值,即可得出结论.
解答:
解:∵不等式ax2+bx+2>0的解集为{x|-
<x<
},
∴-
和
为方程ax2+bx+2=0的两个实根,且a<0,
由韦达定理可得
,
解得a=-12,b=-2,
∴a+b=-14.
故答案为:-14.
| 1 |
| 2 |
| 1 |
| 3 |
∴-
| 1 |
| 2 |
| 1 |
| 3 |
由韦达定理可得
|
解得a=-12,b=-2,
∴a+b=-14.
故答案为:-14.
点评:本题考查一元二次不等式的解集,注意和二次方程的根的关系是解决问题的关键,属基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
为了得到函数y=cos(x-
)的图象,只需把函数y=cosx图象上所有的点( )
| 1 |
| 3 |
A、向左平行移动
| ||
B、向左平行移动
| ||
C、向右平行移动
| ||
D、向右平行移动
|
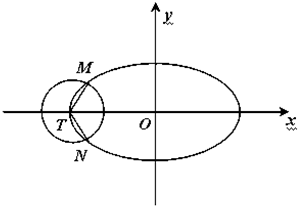 如图,已知椭圆C:
如图,已知椭圆C: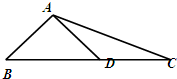 如图,在△ABC中,AD⊥AB,
如图,在△ABC中,AD⊥AB,