题目内容

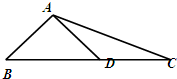如图，在△ABC中，AD⊥AB，
BC
=2
BD
，|
AD
|=1，则
AC
•
AD
的值为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由
AD
⊥
AB
，可得
AD
•
AB
=0，|
BD
|cos∠BDA=|
AD
|=1．利用
AC
•
AD
=(
AB
+
BC
)•
AD
即可得出．
解答： 解：∵
AD
⊥
AB
，∴
AD
•
AB
=0，|
BD
|cos∠BDA=|
AD
|=1．
又
BC
=2
BD
，
∴
AC
•
AD
=(
AB
+
BC
)•
AD
=
AB
•
AD
+
BC
•
AD
=0+2
BD
•
AD
=2|
BD
| |
AD
|cos∠BDA=2．
故答案为：2．
点评：本题考查了向量的三角形法则、共线定理、数量积运算，属于基础题．
练习册系列答案
相关题目
已知
tanα
1-tanα
=-
1
3

（Ⅰ）求
sinα-2cosα
3sinα+cosα
的值；
（Ⅱ）若α∈(0，π)，β∈(0，
π
2
)，cos(2β+α)=
5
5
，求sinβ的值．
在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．若点P为直线ρcosθ-ρsinθ-4=0上一点，点Q为曲线
x=t
y=
1
4
t2
(t为参数）上一点，则|PQ|的最小值为
 
．
正方体ABCD-A1B1C1D1中与A1B是异面直线的棱有
 
条．
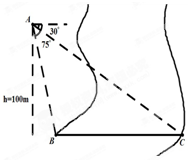如图，在气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，若此时的气球高度是100m，则河流在B，C两地的宽度为
 
．
若不等式ax2+bx+2＞0的解集为{x|-
1
2
＜x＜
1
3
}，则a+b=
 
．
在△ABC中，A=
π
3
，
AP
=2
AB
+
AC
，四边形ABPC的面积为
9
3
2
，则
AB
•
AC
=
 
．
已知双曲线
x2
a2
-
y2
b2
=1的离心率为2，焦点与椭圆
x2
25
+
y2
9
=1的焦点相同，那么双曲线的方程为
 
．
函数y=3x+1（x≥-1）的值域是（　　）
A、（0，+∞）
B、（1，+∞）
C、[0．+∞）
D、[1．+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网