题目内容
18.设集合A={x|-1≤x<4},B={x|x2-4x+3<0},则A∩(∁RB)可表示为( )| A. | [-1,1)∪(3,4) | B. | [-1,1]∪[3,4) | C. | (1,3) | D. | (-∞,+∞) |
分析 化简集合B,求出∁RB,再计算A∩(∁RB).
解答 解:集合A={x|-1≤x<4}=[-1,4),
B={x|x2-4x+3<0}={x|1<x<3}=(1,3),
∴∁RB=(-∞,1]∪[3,+∞);
∴A∩(∁RB)=[-1,1]∪[3,4).
故选:B.
点评 此题考查了交、并、补集的混合运算问题,熟练掌握各自的定义是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
8.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点与虚轴的一个端点构成一个角为120°的三角形,则双曲线C的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
3.设集合A={x|-1≤x<3},B={x|x2-3x+2<0},则A∩(∁RB)可表示为( )
| A. | [-1,1)∪(2,3) | B. | [-1,1]∪[2,3) | C. | (1,2) | D. | (-∞,+∞) |
10.i是虚数单位,复数$\frac{3+4i}{1-2i}$=( )
| A. | 1+2i | B. | 1-2i | C. | -1+2i | D. | -1-2i |
7.在${(x-\frac{1}{2x})^6}$的展开式中,x4的系数为( )
| A. | -3 | B. | $-\frac{1}{2}$ | C. | 3 | D. | 6 |
8.已知集合A={y|y=2x-1,x∈R},B={x|x-x2>0},则A∩B=( )
| A. | (-1,+∞) | B. | (-1,1) | C. | (-1,0) | D. | (0,1) |
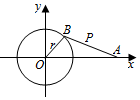 如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.
如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.