题目内容
9.在等腰△ABC中,BD和CE是两腰上的中线,且以BD⊥CE,求cosA.分析 连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,DE为△ABC的中位线,故BC=4x,四边形BCDE为等腰梯形,根据等腰梯形的性质可知,BF=$\frac{1}{2}$(BC-DE)=x,则FC=3x,又△BCG为等腰直角三角形,故△CEF为等腰直角三角形,则EF=CF=3x,解Rt△BEF可求解cos∠BEF,利用二倍角公式可得顶角∠A的余弦值.
解答 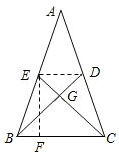 解:如图,连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,
解:如图,连接DE,过E点作EF⊥BC,垂足为F,设DE=2x,
依题意,得DE为△ABC的中位线,∴BC=4x,
又∵四边形BCDE为等腰梯形,
∴BF=$\frac{1}{2}$(BC-DE)=x,则FC=3x,
∵BD⊥CE,
∴△BCG为等腰直角三角形,
∵EF⊥BC,
∴△CEF为等腰直角三角形,
∴EF=CF=3x,
在Rt△BEF中,EF=3x,BF=x,BE=$\sqrt{10}$x,
∴cos∠BEF=$\frac{\sqrt{3}}{10}$,
∴cos∠A=2cos2∠BEF-1=2×$\frac{9}{10}$-1=$\frac{4}{5}$.
点评 本题考查了锐角三角函数值的求法,三角形中位线定理,梯形的性质.求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法,把问题转化到直角三角形中求三角函数值.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
7.函数y=2sin(4x-$\frac{2π}{3}$)的图象( )
| A. | 关于原点对称 | B. | 关于x轴对称 | ||
| C. | 关于直线x=-$\frac{π}{6}$对称 | D. | 关于点($\frac{π}{6}$,0)对称 |
17.直线$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=1-\frac{{\sqrt{3}}}{2}t\end{array}\right.$( t为参数)倾斜角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
14.若方程$\left\{\begin{array}{l}{x=1-3t}\\{y=4t}\end{array}\right.$(t为参数)与$\left\{\begin{array}{l}{x=1+λcosθ}\\{y=λsinθ}\end{array}\right.$(λ为参数)表示同一条直线,则λ与t的关系是( )
| A. | λ=5t | B. | λ=-5t | C. | t=5λ | D. | t=-5λ |
18.设集合A={x|-1≤x<4},B={x|x2-4x+3<0},则A∩(∁RB)可表示为( )
| A. | [-1,1)∪(3,4) | B. | [-1,1]∪[3,4) | C. | (1,3) | D. | (-∞,+∞) |
19.某中学共有学生2000名,校卫生室为了解学生身体健康状况,对全校学生按性别分别采用分层抽样的办法进行抽样调查,抽取了一个容量为200的样本,样本中男生107人,则该中学共有女生( )
| A. | 1070人 | B. | 1030人 | C. | 930人 | D. | 970人 |