题目内容
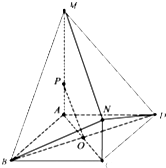 如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3.
如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3.(Ⅰ)若点P在AM上,且MP=2PA,求证:OP∥平面MND;
(Ⅱ)求二面角B-MN-D的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取MP的中点Q,连结CQ,由已知条件得MN∥PO,由此能证明PO∥平面MND.
(Ⅱ)由勾股定理推导出BN⊥MN,根据对称性,同理得DN⊥MN,由已知条件得∠BND为二面角B-MN-D的平面角,由此能求出二面角B-MN-D的余弦值.
(Ⅱ)由勾股定理推导出BN⊥MN,根据对称性,同理得DN⊥MN,由已知条件得∠BND为二面角B-MN-D的平面角,由此能求出二面角B-MN-D的余弦值.
解答:
(Ⅰ)证明:取MP的中点Q,连结CQ,
∵MQ∥NC,MQ=NC=1,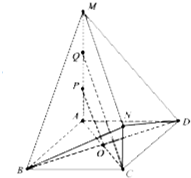
∴MN∥CQ,
∵P是AQ的中点,O是AC的中点,
∴MN∥PO,
∵MN?平面MND,PO不包含于平面MND,
∴PO∥平面MND.
(Ⅱ)解:∵MB=
=
,
MN=
=2
,BN=
=
,
∴MN2+BN2=13,∴BN⊥MN,
根据对称性,同理得DN⊥MN,
∴∠BND为二面角B-MN-D的平面角,
∵BD=2
,BN=ND=
,
∴cosθ=
=-
.
∴二面角B-MN-D的余弦值为-
.
∵MQ∥NC,MQ=NC=1,

∴MN∥CQ,
∵P是AQ的中点,O是AC的中点,
∴MN∥PO,
∵MN?平面MND,PO不包含于平面MND,
∴PO∥平面MND.
(Ⅱ)解:∵MB=
| AB2+MA2 |
| 13 |
MN=
| AC2+(MA-NC)2 |
| 2 |
| CB2+NC2 |
| 5 |
∴MN2+BN2=13,∴BN⊥MN,
根据对称性,同理得DN⊥MN,
∴∠BND为二面角B-MN-D的平面角,
∵BD=2
| 3 |
| 5 |
∴cosθ=
| BN2+ND2-BD2 |
| 2BN•DN |
| 1 |
| 5 |
∴二面角B-MN-D的余弦值为-
| 1 |
| 5 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 如图,在△ABC中,BC=24.AC,AB边上的中线长之和等于39.
如图,在△ABC中,BC=24.AC,AB边上的中线长之和等于39.