题目内容
平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为
，则球O的表面积为 ．
| 2 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：利用平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为
，求出球的半径，然后求解球O的表面积．
| 2 |
解答：
解：因为平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为
，
所以球的半径为：
=
．
所以球O的表面积为4π×3=12π．
故答案为：12π．
| 2 |
所以球的半径为：
| 2+1 |
| 3 |
所以球O的表面积为4π×3=12π．
故答案为：12π．
点评：本题考查球的表面积的求法，考查空间想象能力、计算能力．
练习册系列答案
备战中考寒假系列答案
相关题目
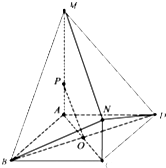如图，四边形ABCD是菱形，且AC=AB=2，AM⊥平面ABCD，MA∥NC，MA=3NC=3．
在如图所示的计算1+5+…+2013的程序框图中，若判断框内为i≤m？，则m的最小值为
