题目内容
已知函数f(x)=alnx-
(a∈R)
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=-
x垂直,求切线方程;
(2)讨论f(x)的单调性;
(3)当a=1,且x≥2时,证明f(x-1)≤2x-5.
| 1 |
| x |
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线y=-
| 1 |
| 2 |
(2)讨论f(x)的单调性;
(3)当a=1,且x≥2时,证明f(x-1)≤2x-5.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求出原函数的导函数,由导数值等于2求得a的值,则切点可求,代入直线方程的点斜式求得切线方程;
(2)求出元函数的导函数,可得当a≥0时导函数在定义域内大于0恒成立,当a<0时求出导函数的零点,由零点对函数的定义域分段,根据导函数在各区间段内的符号得到函数的单调区间;
(3)令g(x)=f(x-1)-(2x-5),求其导函数,得到g′(x)<0,则g(x)在[2,+∞)上递减,从而证得答案.
(2)求出元函数的导函数,可得当a≥0时导函数在定义域内大于0恒成立,当a<0时求出导函数的零点,由零点对函数的定义域分段,根据导函数在各区间段内的符号得到函数的单调区间;
(3)令g(x)=f(x-1)-(2x-5),求其导函数,得到g′(x)<0,则g(x)在[2,+∞)上递减,从而证得答案.
解答:
(1)解:∵f(x)=alnx-
,
∴f′(x)=
+
.
由已知得f′(1)=a+1=2,则a=1,那么切点为(1,-1).
故切线方程为y+1=2(x-1),即2x-y-3=0;
(2)解:由于f′(x)=
+
=
(x>0).
当a≥0时,恒有f′(x)>0,那么f(x)在(0,+∞)上递增;
当a<0时,由f′(x)=0,得x=-
.
若x∈(0,-
),则f′(x)>0,那么f(x)在(0,-
) 递增.
若x∈(-
,+∞),则f′(x)<0,那么f(x)在(-
,+∞)递减;
(3)证明:当a=1时,令g(x)=f(x-1)-(2x-5),
则g(x)=ln(x-1)-
-2x+5.
g′(x)=
+
-2=-
.
当x≥2时,g′(x)<0,则g(x)在[2,+∞)上递减,那么g(x)≤g(2)=0.
故当a=1且x≥2时,f(x-1)≤(2x-5).
| 1 |
| x |
∴f′(x)=
| a |
| x |
| 1 |
| x2 |
由已知得f′(1)=a+1=2,则a=1,那么切点为(1,-1).
故切线方程为y+1=2(x-1),即2x-y-3=0;
(2)解:由于f′(x)=
| a |
| x |
| 1 |
| x2 |
| ax+1 |
| x2 |
当a≥0时,恒有f′(x)>0,那么f(x)在(0,+∞)上递增;
当a<0时,由f′(x)=0,得x=-
| 1 |
| a |
若x∈(0,-
| 1 |
| a |
| 1 |
| a |
若x∈(-
| 1 |
| a |
| 1 |
| a |
(3)证明:当a=1时,令g(x)=f(x-1)-(2x-5),
则g(x)=ln(x-1)-
| 1 |
| x-1 |
g′(x)=
| 1 |
| x-1 |
| 1 |
| (x-1)2 |
| (2x-1)(x-2) |
| (x-1)2 |
当x≥2时,g′(x)<0,则g(x)在[2,+∞)上递减,那么g(x)≤g(2)=0.
故当a=1且x≥2时,f(x-1)≤(2x-5).
点评:本题考查了利用导数求曲线上某点处的切线方程,考查了利用导数研究函数的单调性,训练了利用构造函数法证明不等式,是压轴题.

练习册系列答案
相关题目
抛物线y2=4x的焦点为F,点P(x,y)为该抛物线上的动点,O为坐标原点,则
的最小值是( )
| |PF| |
| |PO| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.
如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I. 如图,圆内接四边形ABCD的对角线BD上有一点E,满足∠BAE=∠CAD.
如图,圆内接四边形ABCD的对角线BD上有一点E,满足∠BAE=∠CAD.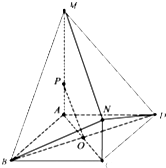 如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3.
如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3.