题目内容
(Ⅰ)设T=
.
(1)已知sin(π-θ)=
,θ为钝角,求T的值;
(2)已知cos(
-θ)=m,θ为钝角,求T的值;
(Ⅱ)已知sinα=
,α是第二象限角,且tan(α+β)=3,求tanβ的值.
| 1+sin2θ |
(1)已知sin(π-θ)=
| 3 |
| 5 |
(2)已知cos(
| π |
| 2 |
(Ⅱ)已知sinα=
| 2 | ||
|
考点:两角和与差的正切函数,三角函数的化简求值
专题:三角函数的求值
分析:(Ⅰ)(1)由条件利用同角三角函数的基本关系求得sinθ=
,cosθ=-
,可得 T=
的值.
(2)由条件利用同角三角函数的基本关系求得sinθ和cosθ的值,可得T=
=|sinθ+cosθ|.再分θ∈(
,
),和θ∈(
,π)两种情况,分别求得T的值.
(Ⅱ)由条件利用同角三角函数的基本关系求得cosα 的值,可得tanα=
的值,再根据 tan(α+β)=
=3,求得tanβ 的值.
| 3 |
| 5 |
| 4 |
| 5 |
| 1+2sinθcosθ |
(2)由条件利用同角三角函数的基本关系求得sinθ和cosθ的值,可得T=
| 1+sin2θ |
| π |
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
(Ⅱ)由条件利用同角三角函数的基本关系求得cosα 的值,可得tanα=
| sinα |
| cosα |
| tanα+tanβ |
| 1-tanα•tanβ |
解答:
解:(Ⅰ)(1)∵sin(π-θ)=
,θ为钝角,可得sinθ=
,cosθ=-
,
∴T=
=
=
=
.
(2)已知cos(
-θ)=sinθ=m,θ为钝角,∴cosθ=-
=-
.
∴T=
=
=|sinθ+cosθ|=|m-
|.
若θ∈(
,
),sinθ+cosθ>0,T=sinθ+cosθ=m-
;
若θ∈(
,π),sinθ+cosθ<0,T=-(sinθ+cosθ )=
-m.
(Ⅱ)已知sinα=
,α是第二象限角,∴cosα=-
=-
,∴tanα=
=-2,
再根据 tan(α+β)=
=
=3,求得tanβ=-1.
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∴T=
| 1+sin2θ |
| 1+2sinθcosθ |
1+2×
|
| 1 |
| 5 |
(2)已知cos(
| π |
| 2 |
| 1-sin2θ |
| 1-m2 |
∴T=
| 1+sin2θ |
| (sinθ+cosθ)2 |
| 1-m2 |
若θ∈(
| π |
| 2 |
| 3π |
| 4 |
| 1-m2 |
若θ∈(
| 3π |
| 4 |
| 1-m2 |
(Ⅱ)已知sinα=
| 2 | ||
|
| 1-sin2α |
| ||
| 5 |
| sinα |
| cosα |
再根据 tan(α+β)=
| tanα+tanβ |
| 1-tanα•tanβ |
| -2+tanβ |
| 1+2tanβ |
点评:本题主要考查同角三角函数的基本关系、两角和的正切公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.
如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.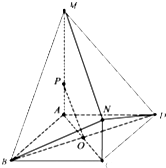 如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3.
如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3. 如图,在△ABC中,
如图,在△ABC中,