题目内容
若向量
，
满足|
|=|
|=1，
与
的夹角为120°，则|2
-
|= ．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由题设条件，可先求|2
-
|2值，再开方求出所求．
| a |
| b |
解答：
解：∵向量
，
满足|
|=|
|=1，
与
的夹角为120°，
∴|2
-
|2=4
2-4
•
+
2=4-4×（-
）+1=7．
∴|2
-
|=
．
故答案为：
| a |
| b |
| a |
| b |
| a |
| b |
∴|2
| a |
| b |
| a |
| a |
| b |
| b |
| 1 |
| 2 |
∴|2
| a |
| b |
| 7 |
故答案为：
| 7 |
点评：本题考查利用数量积的运算求模，此做法是此类题的常用方法，规律：要求模，先求其平方．
练习册系列答案
阅读快车系列答案
相关题目
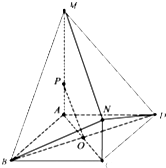如图，四边形ABCD是菱形，且AC=AB=2，AM⊥平面ABCD，MA∥NC，MA=3NC=3．
如图，在△ABC中，