题目内容
在等差数列{an}中,若a10=10,a19=100,前n项和Sn=0,则n= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:利用等差数列的通项公式和前n项和公式求解.
解答:
解:∵在等差数列{an}中,a10=10,a19=100,
∴
,解得a1=-80,d=10,
∴Sn=-80n+
×10=5n2-85n,
∵Sn=0,∴5n2-85n=0,
解得n=17或n=0(舍).
故答案为:17.
∴
|
∴Sn=-80n+
| n(n-1) |
| 2 |
∵Sn=0,∴5n2-85n=0,
解得n=17或n=0(舍).
故答案为:17.
点评:本题考查使得数列的前n项和为0时的项数n的求法,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
要得到函数f(x)=sinx+cosx的图象,可将函数g(x)=sinx-cosx的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
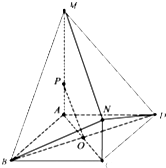 如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3.
如图,四边形ABCD是菱形,且AC=AB=2,AM⊥平面ABCD,MA∥NC,MA=3NC=3.
