题目内容
已知定义在(-1,1)上的奇函数f(x).在x∈(-1,0)时,f(x)=2x+2-x.
(1)试求f(x)的表达式;
(2)用定义证明f(x)在(-1,0)上是减函数;
(3)若对于x∈(0,1)上的每一个值,不等式t•2x•f(x)<4x-1恒成立,求实数t的取值范围.
(1)试求f(x)的表达式;
(2)用定义证明f(x)在(-1,0)上是减函数;
(3)若对于x∈(0,1)上的每一个值,不等式t•2x•f(x)<4x-1恒成立,求实数t的取值范围.
考点:指数函数综合题,奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:(1)由f(x)是定义在(-1,1)上的奇函数可得f(0)=0,x∈(0,1)时,f(x)=-f(-x)=-(2x+2-x);从而写出f(x)的表达式;
(2)取值,作差,化简,判号,下结论五步;
(3)对于x∈(0,1)上的每一个值,不等式t•2x•f(x)<4x-1恒成立转化为对于x∈(0,1)上的每一个值,不等式t>-
恒成立,从而可得.
(2)取值,作差,化简,判号,下结论五步;
(3)对于x∈(0,1)上的每一个值,不等式t•2x•f(x)<4x-1恒成立转化为对于x∈(0,1)上的每一个值,不等式t>-
| 4x-1 |
| 4x+1 |
解答:
解:(1)∵f(x)是定义在(-1,1)上的奇函数,
∴f(0)=0,
设∈(0,1),则-x∈(-1,0),则
f(x)=-f(-x)
=-(2x+2-x),
故f(x)=
;
(2)任取x1,x2∈(-1,0),且x1<x2,
则f(x1)-f(x2)=2x1+2-x1-(2x2+2-x2)
=
,
∵x1<x2<0,
∴2x1-2x2<0,0<2x12x2<1,
故f(x1)-f(x2)>0,
故f(x)在(-1,0)上是减函数;
(3)由题意,t•2x•f(x)<4x-1可化为
t•2x•(-(2x+2-x))<4x-1,
化简可得,t>-
,
令g(x)=-
=-1+
,
∵x∈(0,1),
∴g(x)<-1+
=0,
故对于x∈(0,1)上的每一个值,不等式t•2x•f(x)<4x-1恒成立可化为
t≥0.
∴f(0)=0,
设∈(0,1),则-x∈(-1,0),则
f(x)=-f(-x)
=-(2x+2-x),
故f(x)=
|
(2)任取x1,x2∈(-1,0),且x1<x2,
则f(x1)-f(x2)=2x1+2-x1-(2x2+2-x2)
=
| (2x1-2x2)(2x12x2-1) |
| 2x12x2 |
∵x1<x2<0,
∴2x1-2x2<0,0<2x12x2<1,
故f(x1)-f(x2)>0,
故f(x)在(-1,0)上是减函数;
(3)由题意,t•2x•f(x)<4x-1可化为
t•2x•(-(2x+2-x))<4x-1,
化简可得,t>-
| 4x-1 |
| 4x+1 |
令g(x)=-
| 4x-1 |
| 4x+1 |
| 2 |
| 4x+1 |
∵x∈(0,1),
∴g(x)<-1+
| 2 |
| 40+1 |
故对于x∈(0,1)上的每一个值,不等式t•2x•f(x)<4x-1恒成立可化为
t≥0.
点评:本题考查了函数的性质的综合应用及恒成立问题的处理方法,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=(m2-m-1)xm是幂函数,则f(x)一定( )
| A、是偶函数 |
| B、是奇函数 |
| C、在x∈(-∞,0)上单调递减 |
| D、在x∈(0,+∞)上单调递减 |
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n都相交 |
| B、与m,n都不相交 |
| C、与m,n中至少一条相交 |
| D、至多与m,n中的一条相交 |
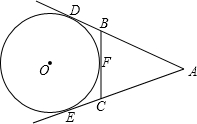 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为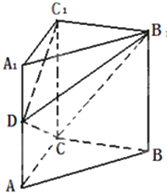 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为棱AA1上的点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为棱AA1上的点.