题目内容
已知函数 f(x)=
(a是常数且a>0).对于下列命题:
①函数f(x)在R上是单调函数;
②函数f(x)的最小值是-1;
③若f(x)>0在[
,+∞)上恒成立,则a的取值范围是a>1;
④对任意的x1<0,x2<0且x1≠x2,恒有f(
)<
.
其中正确命题的序号是 .
|
①函数f(x)在R上是单调函数;
②函数f(x)的最小值是-1;
③若f(x)>0在[
| 1 |
| 2 |
④对任意的x1<0,x2<0且x1≠x2,恒有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:①只需说明函数f(x)在R上的单调性即可;
②由图只需说明在点x=0处函数f(x)的最小值是-1;
③只需说明f(x)>0在[
,+∞)上恒成立,则当x=
时,函数取得最小值,从而求得a的取值范围是a>1;
④已知函数在(-∝,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,故D正确.
②由图只需说明在点x=0处函数f(x)的最小值是-1;
③只需说明f(x)>0在[
| 1 |
| 2 |
| 1 |
| 2 |
④已知函数在(-∝,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,故D正确.
解答:
解:函数 f(x)=
(a是常数且a>0).如下图所示:

①由图象说明函函数f(x)在R上不是单调函数;故错;
②由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
③只需说明f(x)>0在[
,+∞)上恒成立,则当x=
时,函数取得最小值,求得a的取值范围是a>1;故正确;
④已知函数函数在(-∝,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,
即f(
)<
,故正确.
故答案为:②③④.
|

①由图象说明函函数f(x)在R上不是单调函数;故错;
②由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
③只需说明f(x)>0在[
| 1 |
| 2 |
| 1 |
| 2 |
④已知函数函数在(-∝,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,
即f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故答案为:②③④.
点评:本题以命题的真假判断为载体考查了分段函数的单调性,最值,单调性及恒成立问题,难度不大,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=3
的值域为( )
| 1 |
| x-1 |
| A、(0,+∞) |
| B、(0,1)∪(1,+∞) |
| C、{x|x≠1} |
| D、(1,+∞) |
定义在R上的偶函数,f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x1-x2)[f(x2)-f(x1)]>0,则当n∈N*时,有( )
| A、f(-n)<f(n-1)<f(n+1) |
| B、f(n-1)<f(-n)<f(n+1) |
| C、f(n+1)<f(-n)<f(n-1) |
| D、f(n+1)<f(n-1)<f(-n) |
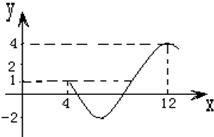 如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.
如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.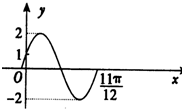 已知函数f(x)=A sin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=A sin(ωx+ϕ)(A>0,ω>0,|φ|<