题目内容
已知数列{an}的通项公式是an=2n-3(
)n,则其前20项和为( )
| 1 |
| 5 |
A、380-
| ||||
B、420-
| ||||
C、400-
| ||||
D、440-
|
考点:数列的求和
专题:等差数列与等比数列
分析:直接分组后由等差数列的前20项和与等比数列的前20项和得答案.
解答:
解:数列{an}的前20项和为:
S20=a1+a2+…+a20=2(1+2+…+20)-3[
+(
)2+…+(
)n]
=2×
-3×
=420-
(1-
).
故选:B.
S20=a1+a2+…+a20=2(1+2+…+20)-3[
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
=2×
| (1+20)×20 |
| 2 |
| ||||
1-
|
| 3 |
| 4 |
| 1 |
| 520 |
故选:B.
点评:本题考查了数列的分组求和,考查了等差数列和等比数列的前n项和,是中档题.

练习册系列答案
相关题目
函数y=3
的值域为( )
| 1 |
| x-1 |
| A、(0,+∞) |
| B、(0,1)∪(1,+∞) |
| C、{x|x≠1} |
| D、(1,+∞) |
已知直线l1与直线l2:3x+4y-6=0平行且与圆:x2+y2+2y=0相切,则直线l1的方程是( )
| A、3x+4y-1=0 |
| B、3x+4y+1=0或3x+4y-9=0 |
| C、3x+4y+9=0 |
| D、3x+4y-1=0或3x+4y+9=0 |
 如图,直角△ABC的斜边AB=2
如图,直角△ABC的斜边AB=2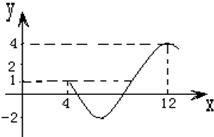 如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.
如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.