题目内容
已知
=(cosα,sinα),
=(cosβ,sinβ),其中0<α<π,0<β<π.
(1)求证:
+
与
-
互相垂直;
(2)若k
+
与
-k
的长度相等,求证:tanα•tanβ=-1(k为非零常数).
| a |
| b |
(1)求证:
| a |
| b |
| a |
| b |
(2)若k
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)首先计算
+
与
-
的积,如果等于0,则互相垂直;
(2)利用长度相等即模相等,得到关于k,α,β的等量关系,求出α,β的关系,得到它们的正切值关系即可.
| a |
| b |
| a |
| b |
(2)利用长度相等即模相等,得到关于k,α,β的等量关系,求出α,β的关系,得到它们的正切值关系即可.
解答:
证明:(1)
+
)(
-
)=
2-
2=cos2α+sin2α-cos2β-sin2β=1-1=0,
所以
+
与
-
互相垂直;
(2)因为k
+
与
-k
的长度相等,所以|k
+
|=|
-k
|,
所以(kcosα+cosβ)2+(ksinα+sinβ)2=(cosα-kcosβ)2+(sinα-ksinβ)2,
整理得,4kcos(α-β)=0,k为非零常数,
所以α-β=kπ+
,
α=β+kπ+
,
tanα•tanβ=tan(β+kπ+
)•tanβ=-cotβtanβ=-1.
| a |
| b |
| a |
| b |
| a |
| b |
所以
| a |
| b |
| a |
| b |
(2)因为k
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
所以(kcosα+cosβ)2+(ksinα+sinβ)2=(cosα-kcosβ)2+(sinα-ksinβ)2,
整理得,4kcos(α-β)=0,k为非零常数,
所以α-β=kπ+
| π |
| 2 |
α=β+kπ+
| π |
| 2 |
tanα•tanβ=tan(β+kπ+
| π |
| 2 |
点评:本题考查了向量的运算以及三角函数的基本关系式的运用,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
函数y=3
的值域为( )
| 1 |
| x-1 |
| A、(0,+∞) |
| B、(0,1)∪(1,+∞) |
| C、{x|x≠1} |
| D、(1,+∞) |
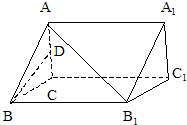 在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=
在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB= 如图,直角△ABC的斜边AB=2
如图,直角△ABC的斜边AB=2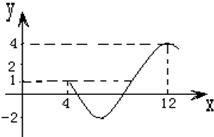 如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.
如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.