题目内容
已知数列{an}的前n项和为Sn,且满足4(n+1)(Sn+1)=(n+2)2an(n∈N+),求an.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:本题可以利用数列{an}的前n项和与通项的关系,将和式转化为项式,再构造新的数列{
}成常数列,通过数列{
}通项研究,得到原数列的通项.
| an |
| (n+1)3 |
| an |
| (n+1)3 |
解答:
解:∵4(n+1)(Sn+1)=(n+2)2an(n∈N+),
∴当n=1时,4(1+1)(S1+1)=(1+2)2a1,
∵S1=a1,∴a1=8.
当n≥2,n∈N*时,
Sn+1=
…①,
Sn-1+1=
…②,
由①-②得:an=
-
,
∴
=
,
∵
=1,
∴数列{
}是首项为1的常数数列,
∴
=1,
∴an=(n+1)3.
∴当n=1时,4(1+1)(S1+1)=(1+2)2a1,
∵S1=a1,∴a1=8.
当n≥2,n∈N*时,
Sn+1=
| (n+2)2an |
| 4(n+1) |
Sn-1+1=
| (n+1)2an-1 |
| 4n |
由①-②得:an=
| (n+2)2an |
| 4(n+1) |
| (n+1)2an-1 |
| 4n |
∴
| an |
| (n+1)3 |
| an-1 |
| n3 |
∵
| a1 |
| (1+1)3 |
∴数列{
| an |
| (n+1)3 |
∴
| an |
| (n+1)3 |
∴an=(n+1)3.
点评:本题考查了数列的前n项和公式与通项公式的关系、构造法求数列通项,还考查了分类讨论的数学思想,本题难度适中,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知m,n是两条不同的直线,α,β是两个不重合的平面,则下列命题正确的是( )
| A、若m∥n,n?α,则m平行于平面α内的任意一条直线 |
| B、若m?α,m∥β,n∥β,则α∥β |
| C、若m⊥α,n⊥β,m∥n,则α∥β |
| D、若α∥β,m?α,n?β,则m∥n |
若数列{an}是等差数列,a3,a10是方程x2-3x-5=0的两根,则a5+a6+a7+a8等于( )
| A、3 | B、4 | C、5 | D、6 |
设f(x)=lg(4-x2),则f(
)+f(
)的定义域是( )
| x |
| 2 |
| 2 |
| x |
| A、(-1,1) |
| B、(-4,4) |
| C、(-4,-1)∪(1,4) |
| D、(-2,-1)∪(1.2) |
若a,b为实数,则“0<ab<1”是“a<
或b>
”的( )条件.
| 1 |
| b |
| 1 |
| a |
| A、充分必要 |
| B、充分而不必要 |
| C、必要而不充分 |
| D、既不充分也不必要 |
在复平面内与复数z=
所对应的点关于虚轴对称的点为A,则A对应的复数为( )
| 5i |
| 1+2i |
| A、1+2i | B、1-2i |
| C、-2+i | D、2+i |
已知集合A={x|y=lg(1-x)},集合B={y|y=x+
,x≠0},则A∩B=( )
| 1 |
| x |
| A、空集∅ |
| B、{x|x<1且x≠0} |
| C、(-∞,-2] |
| D、(-∞,1) |
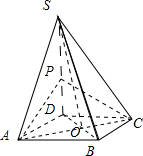 如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.
如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.