题目内容
如图，在正四面体PABC中，若E，F分别在棱PC，AB上，且| |CE| |
| |PC| |
| |AF| |
| |AB| |
| 1 |
| 3 |
考点：异面直线及其所成的角
专题：计算题,空间角
分析：画出立体图形，根据中点找平行线，把所求的异面直线角转化为一个三角形的内角来计算．
解答：
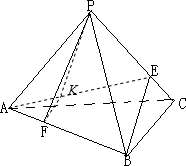解：由题意可得四面体P-ABC为正四面体，
如图，连接AE，AE上取点，使得|AK|：|AE|=1：3，连接FK，则FK∥BE
故∠PFK即为所求的异面直线角或者其补角．
设这个正四面体的棱长为3，在△PKF中，PF=
=BE，KF=
，KE=
，
∴PK=
．
△PKF中，由余弦定理可得 cos∠PFK=
=
故答案为：
．
解：由题意可得四面体P-ABC为正四面体，如图，连接AE，AE上取点，使得|AK|：|AE|=1：3，连接FK，则FK∥BE
故∠PFK即为所求的异面直线角或者其补角．
设这个正四面体的棱长为3，在△PKF中，PF=
| 7 |
| ||
| 3 |
| ||
| 2 |
∴PK=
2
| ||
| 3 |
△PKF中，由余弦定理可得 cos∠PFK=
7+
| ||||||
2•
|
| 3 |
| 7 |
故答案为：
| 3 |
| 7 |
点评：本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力．在立体几何中找平行线是解决问题的一个重要技巧，这个技巧就是通过三角形的中位线找平行线，如果试题的已知中涉及到多个中点，则找中点是出现平行线的关键技巧．
练习册系列答案
名校课堂系列答案
相关题目
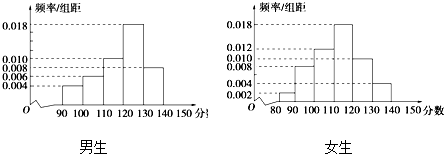
我国政府对PM2.5采用如下标准：