已知函数f(x)=ex+e-x.若曲线y=f(x)的一条切线的斜率为$\frac{3}{2}$.则该切点的横坐标等于( )A．ln2B．2ln2C．2D．$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网——

题目内容

15．已知函数f（x）=e^x+e^-x，若曲线y=f（x）的一条切线的斜率为$\frac{3}{2}$，则该切点的横坐标等于（　　）

A．

ln2

B．

2ln2

C．

2

D．

$\sqrt{2}$

分析求出导数，设出切点，可得切线的斜率，解方程可得切点的横坐标．

解答解：f（x）=e^x+e^-x，
导数为f′（x）=e^x-e^-x，
设切点为（m，n），
则e^m-e^-m=$\frac{3}{2}$，
解得m=ln2，
故选：A．

点评本题考查导数的运用：求切线的斜率，考查转化思想以及运算能力，属于基础题．

练习册系列答案

六月冲刺系列答案

导学全程练创优训练系列答案

课时同步导练系列答案

夺分王系列答案

助学读本系列答案

指南针导学探究系列答案

学习指要系列答案

每课一练浙江少年儿童出版社系列答案

双成卷王系列答案

阳光训练课时作业系列答案

相关题目

5．等差数列{a_n}中，若a₃+a₆+a₉=12，则数列{a_n}的前11项和等于（　　）

6．《张丘建算经》是我国南北朝时期的一部重要数学著作，书中系统的介绍了等差数列，同类结果在三百多年后的印度才首次出现．书中有这样一个问题，大意为：某女子善于织布，后一天比前一天织的快，而且每天增加的数量相同，已知第一天织布5尺，一个月（按30天计算）总共织布585尺，问每天增加的数量为多少尺？该问题的答案为（　　）

$\frac{1}{2}$尺

$\frac{2}{3}$尺

$\frac{3}{2}$尺

3．若$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-1，3），则$\overrightarrow a•\overrightarrow b$=（　　）

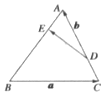如图，△ABC中，$\frac{CD}{DA}=\frac{AE}{EB}=\frac{1}{2}$，记$\overrightarrow{BC}=\overrightarrow{a，}\overrightarrow{CA}=\overrightarrow b$，则$\overrightarrow{DE}$=$\frac{1}{3}（\overrightarrow b-\overrightarrow a）$．（用$\overrightarrow a$和$\overrightarrow b$表示）

20．设$α∈（\frac{π}{2}，π）$，且$sinα（sinα+cosα）=\frac{21}{25}$，则tanα的值为-7．

7．已知双曲线C₁：$\frac{x^2}{16}-\frac{y^2}{4}$=1，双曲线C₂：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，M 是双曲线C₂ 一条渐近线上的点，且OM⊥MF₂，若△OMF₂的面积为 16，且双曲线C₁，C₂的离心率相同，则双曲线C₂的实轴长为（　　）

4．已知cosα=-$\frac{2}{3}$，则$\frac{1}{1+ta{n}^{2}α}$=$\frac{4}{9}$．

2．在长方体ABCD-A₁B₁C₁D₁中，底面ABCD是边长为$\sqrt{2}$的正方形，AA₁=3，E是AA₁的中点，过C₁作C₁F⊥平面BDE与平面ABB₁A₁交于点F，则CF与平面ABCD所成角的正切值为$\frac{5}{6}$．