题目内容
2.在长方体ABCD-A1B1C1D1中,底面ABCD是边长为$\sqrt{2}$的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则CF与平面ABCD所成角的正切值为$\frac{5}{6}$.分析 连结AC、BD,交于点O,当C1F与EO垂直时,C1F⊥平面BDE,从而F∈AA1,进而∠CAF是CF与平面ABCD所成角,由△C1A1F∽△EAO,求出AC,由此能求出CF与平面ABCD所成角的正切值.
解答 解:连结AC、BD,交于点O,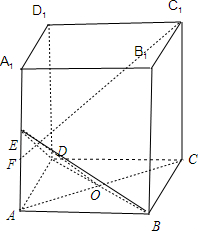
∵四边形ABCD是正方形,AA1⊥底面ABCD,
∴BD⊥平面ACC1A1,
则当C1F与EO垂直时,C1F⊥平面BDE,
∵F∈平面ABB1A1,∴F∈AA1,
∴∠CAF是CF与平面ABCD所成角,
在矩形ACC1A1中,△C1A1F∽△EAO,
则$\frac{{A}_{1}{C}_{1}}{{A}_{1}F}$=$\frac{AE}{AO}$,
∵A1C1=2AO=$\sqrt{2}$AB=2,AE=$\frac{3}{2}$,
∴A1F=$\frac{4}{3}$,∴AF=$\frac{5}{3}$,
∴tan$∠CAF=\frac{AF}{AC}$=$\frac{\frac{5}{3}}{2}$=$\frac{5}{6}$.
∴CF与平面ABCD所成角的正切值为$\frac{5}{6}$.
故答案为:$\frac{5}{6}$.
点评 本题考查线面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
15.已知函数f(x)=ex+e-x,若曲线y=f(x)的一条切线的斜率为$\frac{3}{2}$,则该切点的横坐标等于( )
| A. | ln2 | B. | 2ln2 | C. | 2 | D. | $\sqrt{2}$ |
16.已知△ABC的三内角A、B、C所对的边分别为a、b、c,若c=2bcosA,则此三角形必是( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
20.已知集合A={1,2,3,4},B={2,3,4,5},则A∪B等于( )
| A. | {2,4} | B. | {1,5} | C. | {2,3,4} | D. | {1,2,3,4,5} |
14.函数$f(x)=\frac{{\sqrt{-lnx}}}{{{x^2}-1}}$的定义域为( )
| A. | (-∞,1) | B. | (0,1) | C. | (0,1] | D. | (-∞,-1)∪(-1,1) |
12.在四棱锥P-ABCD中,PA⊥底面ABCD,其中PA=2AB=2AD=2,G为三角形BCD的重心,则PG与底面ABCD所成角的正弦值为( )
| A. | $3\sqrt{2}$ | B. | $\frac{3\sqrt{11}}{11}$ | C. | $\frac{{\sqrt{19}}}{19}$ | D. | $\frac{{3\sqrt{19}}}{19}$ |