题目内容

5．等差数列{an}中，若a3+a6+a9=12，则数列{an}的前11项和等于（　　）
A．22B．33C．44D．55

分析 由等差数列{an}的性质可得：a3+a6+a9=12=3a6，可得a6．再利用求和公式及其性质即可得出．

解答 解：由等差数列{an}的性质可得：a3+a6+a9=12=3a6，可得a6=4．
则数列{an}的前11项和=$\frac{11（{a}_{1}+{a}_{11}）}{2}$=11a6=44．
故选：C．

点评 本题考查了等差数列的通项公式性质与求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
15．已知集合$M=\left\{{\left.{（{x，y}）}\right|\left\{\begin{array}{l}2x+y=2\\ x-y=1\end{array}\right.}\right\}$，则（　　）
A．M={1，0}B．M={（1，0）}C．M=（1，0）D．M={1}
16．下列判断中，正确的有（　　）
①一个命题的逆命题为真，它的否命题也一定为真；
②在△ABC中，“∠B=60°”是“∠A，∠B，∠C三个角成等差数列”的充要条件；
③$\left\{{\begin{array}{l}{x＞1}\\{y＞2}\end{array}}\right.$是$\left\{{\begin{array}{l}{x+y＞3}\\{xy＞2}\end{array}}\right.$的充要条件；
④“am2＜bm2”是“a＜b”的必要不充分条件．
A．①②B．①③C．①④D．②③
13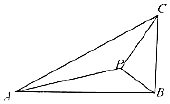．如图所示，P为△ABC内一点，且满足△ABC∽△CPB，∠ABC=∠CPB=90°，$AB=2\sqrt{3}$，BC=2，则PA=（　　）
A．7B．$\sqrt{5}$C．$\sqrt{7}$D．$\sqrt{19}$
20．已知数列{an}的前n项和为Sn，且满足an+Sn=1．
（1）求数列{an}的通项公式；
（2）令bn=n•an，求数列{bn}的前n项和Tn．
10．设集合A={-2，-1，0，1，2}，B={x|x2+2x＜0}，则A∩B=（　　）
A．{1，2}B．{-2，-1}C．{-1}D．{-2，-1，0}
17．已知等差数列{an}中，a5=9，且2a3-a2=6，则a1等于（　　）
A．-2B．-3C．0D．1
14．已知抛物线C1：y2=4x的焦点到双曲线C2：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线的距离为$\frac{{\sqrt{3}}}{3}$，则双曲线C2的离心率为$\frac{{\sqrt{6}}}{2}$．
15．已知函数f（x）=ex+e-x，若曲线y=f（x）的一条切线的斜率为$\frac{3}{2}$，则该切点的横坐标等于（　　）
A．ln2B．2ln2C．2D．$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网