题目内容

3．若$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-1，3），则$\overrightarrow a•\overrightarrow b$=（　　）
A．2B．1C．0D．-1

分析 利用平面向量的数量积公式求解．

解答 解：∵$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-1，3），
∴$\overrightarrow a•\overrightarrow b$=-2+3=1．
故选：B．

点评 本题考查向量的数量积的求法，是基础题，解题时要认真审题，注意向量的数量积公式的合理运用．

练习册系列答案
相关题目
13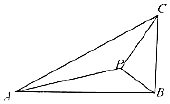．如图所示，P为△ABC内一点，且满足△ABC∽△CPB，∠ABC=∠CPB=90°，$AB=2\sqrt{3}$，BC=2，则PA=（　　）
A．7B．$\sqrt{5}$C．$\sqrt{7}$D．$\sqrt{19}$
14．已知抛物线C1：y2=4x的焦点到双曲线C2：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线的距离为$\frac{{\sqrt{3}}}{3}$，则双曲线C2的离心率为$\frac{{\sqrt{6}}}{2}$．
11．在△ABC中，A，B，C的对边分别为a，b，c，若2（a2+c2）-ac=2b2，则sinB=（　　）
A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{{\sqrt{15}}}{4}$D．$\frac{{\sqrt{3}}}{2}$
18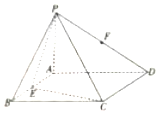．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是矩形，且PA=AD=3，$CD=\sqrt{6}$，E、F分别是AB、PD的中点，则点F到平面PCE的距离为（　　）
A．$\frac{{3\sqrt{2}}}{4}$B．$\sqrt{2}$C．$\frac{{3\sqrt{3}}}{4}$D．$\frac{{\sqrt{3}}}{2}$
8．下列四个不等式中，错误的个数是（　　）
①50.5＜60.5②0.10.3＜0.10.4③log23＜log25④log32＜0.1-0.2．
A．0B．1C．2D．3
15．已知函数f（x）=ex+e-x，若曲线y=f（x）的一条切线的斜率为$\frac{3}{2}$，则该切点的横坐标等于（　　）
A．ln2B．2ln2C．2D．$\sqrt{2}$
12．一个几何体的三视图如图所示，则该几何体的体积为（　　）
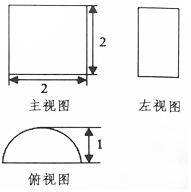
A．πB．2πC．2π+4D．3π+4
13．已知动点P到点M（-1，0）的距离与它到直线x=1的距离相等．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）若直线l：x+y+1=0与动点P的轨迹交于A，B两点，求弦AB的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网