题目内容
4.已知cosα=-$\frac{2}{3}$,则$\frac{1}{1+ta{n}^{2}α}$=$\frac{4}{9}$.分析 利用商的关系化切为弦得答案.
解答 解:∵cosα=-$\frac{2}{3}$,
∴$\frac{1}{1+ta{n}^{2}α}$=$\frac{1}{1+\frac{si{n}^{2}α}{co{s}^{2}α}}=\frac{1}{\frac{si{n}^{2}α+co{s}^{2}α}{co{s}^{2}α}}=co{s}^{2}α=\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
点评 本题考查三角函数的化简求值,考查了同角三角函数基本关系式的应用,是基础的计算题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
15.已知函数f(x)=ex+e-x,若曲线y=f(x)的一条切线的斜率为$\frac{3}{2}$,则该切点的横坐标等于( )
| A. | ln2 | B. | 2ln2 | C. | 2 | D. | $\sqrt{2}$ |
12.一个几何体的三视图如图所示,则该几何体的体积为( )
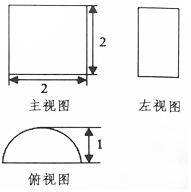

| A. | π | B. | 2π | C. | 2π+4 | D. | 3π+4 |
9.已知函数f(x)=cos(2x-$\frac{π}{6}$)(x∈R),下列命题正确的是( )
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | B. | f(x)的图象关于点($\frac{π}{12}$,0)对称 | ||
| C. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | f(x)在区间(-$\frac{π}{3}$,$\frac{π}{12}$)上是增函数 |
16.已知△ABC的三内角A、B、C所对的边分别为a、b、c,若c=2bcosA,则此三角形必是( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |