题目内容
20.设$α∈(\frac{π}{2},π)$,且$sinα(sinα+cosα)=\frac{21}{25}$,则tanα的值为-7.分析 由已知利用同角三角函数基本关系式化简可求4tan2α+25tanα-21=0,结合α的范围,即可计算得解.
解答 解:∵$sinα(sinα+cosα)=\frac{21}{25}$,
∴$\frac{si{n}^{2}α+sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{21}{25}$,即:$\frac{ta{n}^{2}α+tanα}{ta{n}^{2}α+1}$=$\frac{21}{25}$,
∴整理可得:4tan2α+25tanα-21=0,
∴解得:tanα=$\frac{3}{4}$,或-7,
∵$α∈(\frac{π}{2},π)$,
∴tanα<0,可得:tanα=-7.
故答案为:-7.
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
10.设集合A={-2,-1,0,1,2},B={x|x2+2x<0},则A∩B=( )
| A. | {1,2} | B. | {-2,-1} | C. | {-1} | D. | {-2,-1,0} |
11.在△ABC中,A,B,C的对边分别为a,b,c,若2(a2+c2)-ac=2b2,则sinB=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
15.已知函数f(x)=ex+e-x,若曲线y=f(x)的一条切线的斜率为$\frac{3}{2}$,则该切点的横坐标等于( )
| A. | ln2 | B. | 2ln2 | C. | 2 | D. | $\sqrt{2}$ |
5.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
| A. | $2\frac{1}{18}$ | B. | $2\frac{1}{17}$ | C. | $2\frac{2}{17}$ | D. | $2\frac{1}{9}$ |
12.一个几何体的三视图如图所示,则该几何体的体积为( )
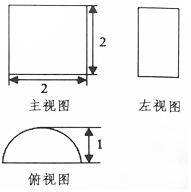

| A. | π | B. | 2π | C. | 2π+4 | D. | 3π+4 |
9.已知函数f(x)=cos(2x-$\frac{π}{6}$)(x∈R),下列命题正确的是( )
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | B. | f(x)的图象关于点($\frac{π}{12}$,0)对称 | ||
| C. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | f(x)在区间(-$\frac{π}{3}$,$\frac{π}{12}$)上是增函数 |