题目内容
13.关于直线a,b,c以及平面α,β,给出下列命题:①若a∥α,b∥α,则a∥b
②若a∥α,b⊥α,则a⊥b
③若a?α,b?α,且c⊥a,c⊥b,则c⊥α
④若a⊥α,a∥β,则α⊥β
其中正确的命题是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
分析 ①,若a∥α,b∥α,则a与b位置关系有相交、异面、平行
②,设β为过a的平面,且α∩β=l.由a∥α,得a∥l.由b⊥l,得b⊥a.
③,根据线面垂直的判定定理,可判断;
④,由直线a∥平面α,各平面α中必存在一条直线b与直线a平行,由此根据直线a⊥平面β,利用平面与平面垂直的判定定理得α⊥β.
解答 解:对于①,若a∥α,b∥α,则a与b位置关系有相交、异面、平行,故错;
对于②,设β为过a的平面,且α∩β=l.∵a∥α,∴a∥l.∵直线b⊥平面α,l?α,∴b⊥l,∴b⊥a.故a⊥b.故正确;
对于③,若a?α,b?α,a∥b,c⊥a,c⊥b时,由于a、b不一定相交,故c⊥α不一定成立,故③错误;
对于④,∵直线a∥平面α,∴平面α中必存在一条直线b与直线a平行,∵直线a⊥平面β,∴直线b⊥平面β,∴α⊥β.故正确;
故选:C
点评 本题以命题的真假判断为载体,考查了空间直线和平面的位置关系,熟练掌握空间线面关系的判定定理,性质定理和几何特征是解答的关键.

练习册系列答案
相关题目
12.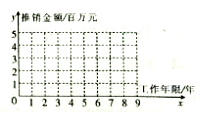 某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:
某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:
(1)请在如图中画出上表数据的散点图;
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若某推销员工作年限为11年,试估计他的年推销金额.
 某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:
某电脑公司有5名产品推销员,其中工作年限与年推销金额数据如下表:| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x(年) | 3 | 5 | 6 | 7 | 9 |
| 推销金额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若某推销员工作年限为11年,试估计他的年推销金额.
8.P为双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$右支上一点,F1,F2分别为双曲线的左、右焦点,且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,直线PF2交y轴于点A,则△AF1P的内切圆半径为( )
| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{{\sqrt{13}}}{2}$ |
5.用反证法证明命题“设a,b为实数,则方程x2+ax+b=0没有实数根”时,要做的假设是( )
| A. | 方程x2+ax+b=0至多有一个实根 | B. | 方程x2+ax+b=0至少有一个实根 | ||
| C. | 方程x2+ax+b=0至多有两个实根 | D. | 方程x2+ax+b=0恰好有两个实根 |
2.已知△ABC中,$a=\sqrt{2},b=\sqrt{3},A={45°}$,则三角形的解的个数( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个或1个 |
3.复数$\frac{3+4i}{{{{(1-i)}^2}}}$=( )
| A. | $-2+\frac{3}{2}i$ | B. | $-2-\frac{3}{2}i$ | C. | $2+\frac{3}{2}i$ | D. | $2-\frac{3}{2}i$ |
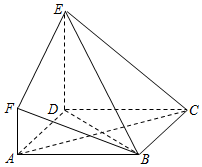 如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°
如图所示多面体中,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°