Question

18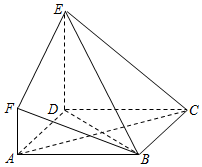．如图所示多面体中，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°
（Ⅰ）作出题中多面体的三视图，并标出相应长度
（Ⅱ）求证：AC⊥平面BDE
（Ⅲ）设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．

Answer 1

分析 （I）根据∠DBE=60°计算DE，再作出三视图即可；
（II）由DE⊥平面ABCD得出DE⊥AC，结合BD⊥AC得出AC⊥平面BDE；
（III）利用平行线等分线段成比例定理即可得出M为BD的三等分点，再给出证明即可．

解答 解：（Ⅰ）作出三视图如图所示：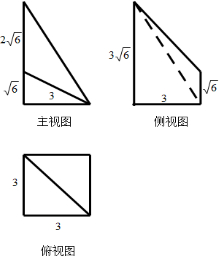


（Ⅱ）证明：因为DE⊥平面ABCD，AC?平面ABCD，
所以DE⊥AC．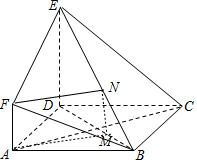
因为底面ABCD是正方形，
所以AC⊥BD，又BD∩DE=D，BD，DE?平面BDE，
∴AC⊥平面BDE．
（Ⅲ）解：在BE上取得N，在BD上取点M，使得$\frac{BM}{BD}=\frac{BN}{BE}=\frac{1}{3}$，
连结MN，FN，AM，
则MN∥DE，$\frac{MN}{DE}$=$\frac{1}{3}$，又AF∥DE，AF=$\frac{1}{3}$DE，
∴AF$\stackrel{∥}{=}$MN，
∴四边形AMNF是平行四边形，
∴AM∥FN，又FN?平面BEF，AM?平面BEF，
∴AM∥平面BEF．
∴当M为BD靠近B的三点分点时，AM∥平面BEF．

点评 本题考查了棱锥的结构特征和三视图，线面垂直、平行的判定，属于中档题．